
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)是否存在不平行于AB的直线l与(I)中椭圆交于不同两点M、N,使(![]() )·
)·![]() =0?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
=0?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
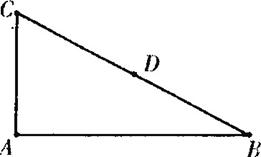
解:(Ⅰ)以AB所在的直线为x轴,AB的垂直平分线为y轴建立
直角坐标系,则A(![]() ,0),B(
,0),B(![]() ,0),C(
,0),C(![]() ),D(0,
),D(0,![]() ).
).
设椭圆方程为为![]() =1 (a>b>0),c=
=1 (a>b>0),c=![]() ,
,
于是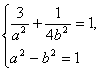 解得
解得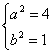 ,
,
∴所求椭圆方程为![]() +y2=1.
+y2=1.
(Ⅱ)∵条件(![]() )·
)·![]() =0等价于|
=0等价于|![]() |=|
|=|![]() |,
|,
∴若存在符合条件的直线,该直线的斜率一定存在,否则与点D(0,![]() )不在x轴上矛盾.∴可设直线l:y=kx+m(k≠0),
)不在x轴上矛盾.∴可设直线l:y=kx+m(k≠0),
由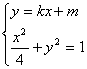 得(1+4k2)x2+8kmx+4m2-4=0,
得(1+4k2)x2+8kmx+4m2-4=0,
由△=64k2m2-4(1+4k2)(4m2-4)>0得4k2+1>m2.
设M(x1,y1),N(x2,y2),MN的中点为Q(x0,y0),
则x0=![]() , y0=kx0+m=
, y0=kx0+m=![]() .
.
∵![]() ,∴
,∴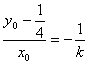 ,即
,即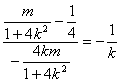 .
.
解得:m=![]() (1+4k2).
(1+4k2).
(将点的坐标代入(![]() )·
)·![]() =0亦可得到此结果)
=0亦可得到此结果)
由4k2+1>m2得,4k2+1>![]() (1+4k2)2得,4k2<143,
(1+4k2)2得,4k2<143,
∴k∈(![]() ,0)∪(0,
,0)∪(0,![]() ).
).
∴存在满足条件的直线l,其斜率的取值范围是(![]() ,0)∪(0,
,0)∪(0,![]() ).
).


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
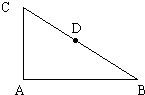 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,|AB|=2
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,|AB|=2| 3 |
| 1 |
| 2 |
| DM |
| DN |
| MN |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
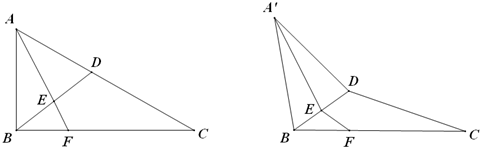
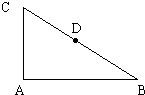 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,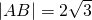 ,
,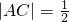 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C.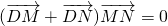 ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com