
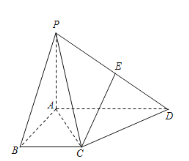
【题目】在四棱锥![]() 中,
中,![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,点E是线段PD的中点.
,点E是线段PD的中点.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面PAB;
平面PAB;
![]() Ⅱ
Ⅱ![]() 求证:平面
求证:平面![]() 平面PCD;
平面PCD;
![]() Ⅲ
Ⅲ![]() 当直线PC与平面PAD所成的角大小为
当直线PC与平面PAD所成的角大小为![]() 时,求线段PA的长.
时,求线段PA的长.
【答案】(I) 证明见解析 (II) 证明见解析(III)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 取线段PA的中点F,连接EF、BF,得出
取线段PA的中点F,连接EF、BF,得出![]() ,四边形BCEF是平行四边形,
,四边形BCEF是平行四边形,
即证![]() ,得出
,得出![]() 平面PAB;
平面PAB;
![]() Ⅱ
Ⅱ![]() 由题意得出
由题意得出![]() ,
,![]() ,可证
,可证![]() 平面PAC,从而证明平面
平面PAC,从而证明平面![]() 平面PCD;
平面PCD;
![]() Ⅲ
Ⅲ![]() 取线段AD中点H,连接CH、PH,可得
取线段AD中点H,连接CH、PH,可得![]() ,
,![]() ,即证
,即证![]() 平面PAD;得出
平面PAD;得出![]() 是直线PC与平面PAD所成的角,从而求得PA的值.
是直线PC与平面PAD所成的角,从而求得PA的值.
![]() Ⅰ
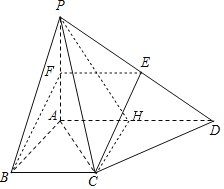
Ⅰ![]() 证明:取线段PA的中点F,连接EF、BF,
证明:取线段PA的中点F,连接EF、BF,
则![]() ,且
,且![]() ,
,
所以四边形BCEF是平行四边形,
所以![]() ;
;
又![]() 平面PAB,
平面PAB,![]() 平面PAB,
平面PAB,
所以![]() 平面PAB;
平面PAB;
![]() Ⅱ
Ⅱ![]() 证明:由题意得,
证明:由题意得,![]() ,又
,又![]() ,
,
所以![]() ;
;
又![]() 平面ABCD,
平面ABCD,
所以![]() ,且
,且![]() ,
,
所以![]() 平面PAC,
平面PAC,
又![]() 平面PCD,
平面PCD,
所以平面![]() 平面PCD;
平面PCD;
![]() Ⅲ
Ⅲ![]() 解:取线段AD中点H,连接CH、PH,
解:取线段AD中点H,连接CH、PH,
可得![]() ,
,![]() ,且
,且![]() ,
,
所以![]() 平面PAD;
平面PAD;
所以![]() 是直线PC与平面PAD所成的角,
是直线PC与平面PAD所成的角,
所以![]() ;
;
所以![]() ;
;
又![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面立角坐标系![]() 中,过点
中,过点![]() 的圆的圆心
的圆的圆心![]() 在
在![]() 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为![]() 的直线
的直线![]() 相切.
相切.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,求经过
,求经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣a)ex(a∈R).
(1)若函数f(x)有两个不同的极值点,求实数a的取值范围;
(2)当a=0时,若关于x的方程f(x)=m存在三个不同的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com