已知函数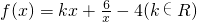 ,且
,且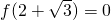 ,则
,则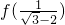 的值等于
的值等于
- A.
8
- B.
-8
- C.
4
- D.
-4
B
分析:构造函数g(x)=f(x)+4=kx+

,易判断g(x)为奇函数,

=-(2+

),由奇函数的性质即可解得.
解答:令g(x)=f(x)+4=kx+

,
因为g(-x)=-kx-

=-g(x),所以g(x)为定义域内的奇函数.
则g[-(2+

)]=-g(2+

),即f[-(2+

)]+4=-[f(2+

)+4],
又
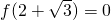
,所以f[-(2+

)]=-8,
因为
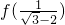
=f[-(2+

)],所以
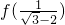
=-8,
故选B.
点评:本题考查函数解析式的求法,本题通过构造函数巧妙利用函数奇偶性避免了繁琐的计算,本题也可先求出解析式再求值.
练习册系列答案
相关习题
科目:高中数学
来源:2013-2014学年广东省高三上学期期中考试理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2013届广东省山一高二下学期第一次段考理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2011-2012学年大纲版高三上学期单元测试(4)数学试卷
题型:选择题
已知函数
 ,且
,且 ,则
,则
的值为 (
)
A.2005 B.2006 C.2007
D..2008
查看答案和解析>>
科目:高中数学
来源:2010年吉林省长春市高二上学期期中考试数学理卷
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2010-2011年浙江省高二下学期第一次质量检测数学理卷
题型:选择题
已知函数 ,且
,且 ,则
,则 的值为 ( )
的值为 ( )
(A)
1 (B)
2 (C) (D)任意正数
(D)任意正数
查看答案和解析>>

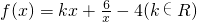 ,且
,且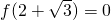 ,则
,则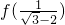 的值等于
的值等于 阅读快车系列答案
阅读快车系列答案
 ,且
,且 ,则
,则