
对任意x1,x2∈R,当x1≠x2时,函数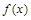 都满足不等式
都满足不等式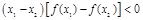 ,若函数
,若函数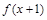 为奇函数,则不等式
为奇函数,则不等式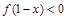 的解集为 ( )
的解集为 ( )
A.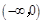 | B. |
C.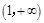 | D.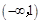 |
科目:高中数学 来源: 题型:单选题
在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x),一种是平均价
格曲线y=g(x)(如f(2)=3表示开始交易后第2小时的即时价格为3元;g(2)=4表示开始交
易后两个小时内所有成交股票的平均价格为4元).下面所给出的四个图象中,实线表示
y=f(x),虚线表示y=g(x),其中可能正确的是 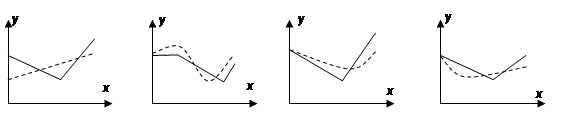
A. B. C. D.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某商场对顾客实行购物优惠活动,规定一次购物付款总额:①如果不超过200元,则不予优惠,②如果超过200元但不超过500元,则按标价给予9折优惠,③如果超过500元,其500元按②条给予优惠,超过500元的部分给予7折优惠.某人两次去购物,分别付款168元和423元,假设他一次购买上述同样的商品,则应付款( )
| A.413.7元 | B.513.7元 | C.546.6元 | D.548.7元 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
函数y=x2-2x的定义域为{0,1,2,3},那么其值域为( )
| A.{-1,0,3} | B.{0,1,2,3} |
| C.{y|-1≤y≤3} | D.{y|0≤y≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com