
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 5 | 10 | 15 | 47 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 2 | 3 | 10 | y | 2 |
| 女士 | 男士 | 总计 | |
| 网购达人 | 50 | 5 | 55 |
| 非网购达人 | 30 | 15 | 45 |
| 总计 | 80 | 20 | 100 |
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (Ⅰ)根据分层抽样方法求出x、y的值,利用列举法计算基本事件数,求出对应的概率;
(Ⅱ)列出2×2列联表,计算观测值K2,对照表中数据,判断结论是否成立即可.
解答 解:(Ⅰ)依题意,女性应抽取80名,男性应抽取20名 …(1分)
∴x=80-(5+10+15+47)=3…(2分)
y=20-(2+3+10+2)=3…(3分)
抽出的100名且消费金额在[800,1000](单位:元)的网购者中有三位女性设为A,B,C;两位男性设为a,b,从5人中任选2人的基本事件有:(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b)共10件…(4分)
设“选出的两名网购者恰好是一男一女”为事件A
事件A包含的基本事件有:(A,a),(A,b),(B,a),(B,b),(C,a),(C,b)共6件…(5分)∴$P(A)=\frac{6}{10}=\frac{3}{5}$…(6分)
(Ⅱ)2×2列联表如下表所示
| 女性 | 男性 | 总计 | |
| 网购达人 | 50 | 5 | 55 |
| 非网购达人 | 30 | 15 | 45 |
| 总计 | 80 | 20 | 100 |
点评 本题考查了分层抽样方法的应用问题,也考查了2×2列联表的应用问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | (-1,3) | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | B. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | ||
| C. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递减 | D. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {0,2} | C. | {0,-2} | D. | {2,0,-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
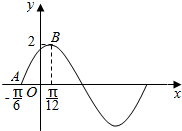 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$
(1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com