
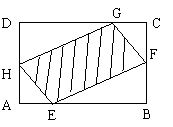
 如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(1)写出y关于x的函数关系式,并指出这
个函数的定义域.
(2)当AE为何值时,绿地面积最大?
科目:高中数学 来源: 题型:
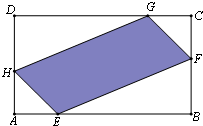 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.写出y关于x的函数关系式,并指出这个函数的定义域.
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.写出y关于x的函数关系式,并指出这个函数的定义域.查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省天水市高三第二次学段考试理科数学试卷(解析版) 题型:解答题
(本题满分12分) 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB= (
( >2),BC=2,且AE=AH=CF=CG,设AE=
>2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为 .
.

(1)写出 关于
关于 的函数关系式,并指出这个函数的定义域;
的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积 最大? (10分)
最大? (10分)
查看答案和解析>>
科目:高中数学 来源:2010年河北省高一上学期期中考试数学试卷 题型:解答题
(本小题满分12分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB= (
( 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为 .
.
(1)写出 关于
关于 的函数关系式,指出这个函数的定义域.
的函数关系式,指出这个函数的定义域.
(2)当AE为何值时,绿地面积最大?
查看答案和解析>>
科目:高中数学 来源:2010-2011年云南省高一上学期期末数学试卷 题型:解答题
(12分)
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB= (
( 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为 .
.
(1)写出 关于
关于 的函数关系式,指出这个函数的定义域.
的函数关系式,指出这个函数的定义域.

(2)当AE为何值时,绿地面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com