
如图,四棱锥 的底面是矩形,
的底面是矩形, 底面
底面 ,
, 为
为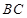 边的中点,
边的中点, 与平面
与平面 所成的角为
所成的角为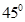 ,且
,且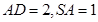 。
。
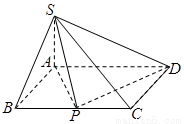
(1)求证: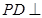 平面
平面
(2)求二面角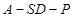 的大小的正切值.
的大小的正切值.
(1)见解析(2)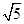
【解析】本试题主要是考查了立体几何中线面垂直的证明与二面角的平面角的求解。
(1)因为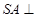 底面
底面 ,
,
所以,∠SBA是SB与平面ABCD所成的角
由已知∠SBA=45°,所以AB=SA=1 易求得,AP=PD= ,
,
又因为AD=2,所以AD2=AP2+PD2,所以 ,从而根据线面垂直的判定定理得到。
,从而根据线面垂直的判定定理得到。
(2)
由于SA⊥底面ABCD,且SA 平面SAD,
平面SAD,
则平面SAD⊥平面PAD
因为PQ⊥AD,所以PQ⊥平面SAD
过Q作QR⊥SD,垂足为R,连结PR,
由三垂线定理可知PR⊥SD,
所以∠PRQ是二面角A-SD-P的平面角,然后接合直角三角形得到求解。
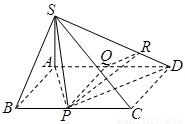
证明:(1)因为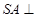 底面
底面 ,
,
所以,∠SBA是SB与平面ABCD所成的角……………….1分
由已知∠SBA=45°,所以AB=SA=1 易求得,AP=PD= ,…….2分
,…….2分
又因为AD=2,所以AD2=AP2+PD2,所以 .……….3分
.……….3分
因为SA⊥底面ABCD,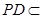 平面ABCD,
平面ABCD,
所以SA⊥PD, ……………....4分
由于SA∩AP=A 所以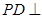 平面SAP.………………… 5分
平面SAP.………………… 5分
(2)设Q为AD的中点,连结PQ, ……………………………6分
由于SA⊥底面ABCD,且SA 平面SAD,
平面SAD,
则平面SAD⊥平面PAD……..7分
因为PQ⊥AD,所以PQ⊥平面SAD
过Q作QR⊥SD,垂足为R,连结PR,
由三垂线定理可知PR⊥SD,
所以∠PRQ是二面角A-SD-P的平面角.…9分
容易证明△DRQ∽△DAS,则 因为DQ=1,SA=1,
因为DQ=1,SA=1, ,
,
所以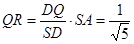 …….10分 在Rt△PRQ中,因为PQ=AB=1,
…….10分 在Rt△PRQ中,因为PQ=AB=1,
所以 所以二面角A-SD-P的大小的正切值为
所以二面角A-SD-P的大小的正切值为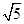 .13分
.13分


科目:高中数学 来源: 题型:
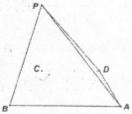
(09年山东实验中学诊断三理)(13分)如图:四棱锥![]() 的底面
的底面![]() 是提醒,腰
是提醒,腰![]() ,
,![]() 平分
平分![]() 且与
且与![]() 垂直,侧面
垂直,侧面![]() 都垂直于底面,平面
都垂直于底面,平面![]() 与底面
与底面![]() 成60°角
成60°角
![]() (1)求证:
(1)求证:![]() ;
;
![]() (2)求二面角
(2)求二面角![]() 的大小
的大小![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三第八次月考文科数学试卷 题型:解答题
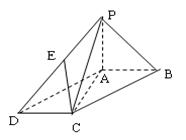
如图,四棱锥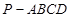 的底面是平行四边形,
的底面是平行四边形,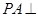 平面
平面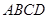 ,
,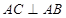 ,
,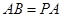 ,
,
点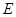 是
是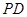 上的点,且
上的点,且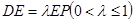 .
.
(Ⅰ)求证: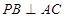 ;
;
(Ⅱ)求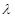 的值,使
的值,使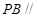 平面
平面 ;
;
(Ⅲ)当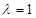 时,求三棱锥
时,求三棱锥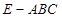 与四棱锥
与四棱锥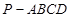 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期摸底理科数学 题型:解答题
((本小题满分14分)如图,四棱锥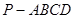 的底面
的底面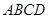 是正方形,侧棱
是正方形,侧棱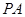
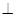 底面
底面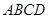 ,
,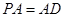 ,
,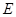 、
、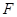 分别是棱
分别是棱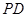 、
、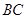 的中点.
的中点.
(1)求证: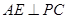 ; (2) 求直线
; (2) 求直线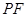 与平面
与平面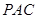 所成的角的正切值
所成的角的正切值
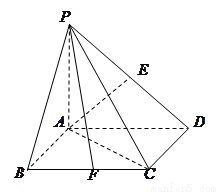
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省成都市高二3月月考数学试卷 题型:填空题
(本小题满分12 分)
如图,四棱锥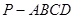 的底面是边长为
的底面是边长为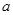 的菱形,
的菱形,
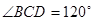 ,
,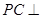 平面
平面 ,
,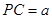 ,
,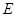 为
为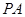 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;
(1)求证:平面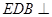 平面
平面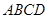 ;
;
(2)求二面角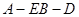 的正切值。
的正切值。
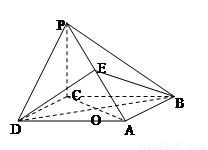
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com