
科目:高中数学 来源: 题型:
已知向量集合M={a|a=(1,2)+λ1(3,4),λ1∈R},N={b|b=(-2,-2)+λ2(4,5),λ2∈R},则M∩N=________.
查看答案和解析>>
科目:高中数学 来源:2013届河北衡水中学高二第二学期期末文科数学试卷(解析版) 题型:选择题
已知=2,=3,=4,…,若=6,(a,t均为正实数),则类比以上等式,可推测a,t的值,a+t=( )
A.35 B.40 C.41 D.42
查看答案和解析>>
科目:高中数学 来源:2013届广东省六校联合体高二元月联考理科数学(解析版) 题型:填空题
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在x=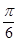 取得最大值2,且函数
取得最大值2,且函数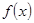 的最小正周期为2
的最小正周期为2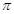 .现将函数y=f(x)图象上各点的横坐标缩小为原来的
.现将函数y=f(x)图象上各点的横坐标缩小为原来的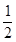 ,纵坐标不变,再把函数图像向右平移
,纵坐标不变,再把函数图像向右平移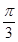 个单位,得到函数y=g(x)的图象,则
个单位,得到函数y=g(x)的图象,则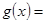
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)已知函数f(x)=sin2x+sinxcosx-(x∈R).
(1) 若x∈,求f(x)的最大值;
(2) 在△ABC中,若A<B,f(A)=f(B)=,求的值.
查看答案和解析>>
科目:高中数学 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点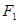 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com