
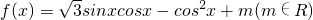 的图象过点M(
的图象过点M( ,0).
,0). sin2x,cos2x=
sin2x,cos2x= (1+cos2x)
(1+cos2x)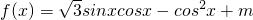 =
= sin2x-
sin2x- (1+cos2x)+m
(1+cos2x)+m sin2x-
sin2x- cos2x-
cos2x- +m=sin(2x-
+m=sin(2x- )-
)- +m
+m ,0),
,0), -
- )-
)- +m=0,解之得m=
+m=0,解之得m=
 ,得B=
,得B=
 ),
), ),其中A∈(0,
),其中A∈(0, )
) <2A-
<2A- <
< ,
, )>sin(-
)>sin(- )=-
)=- ,sin(2A-
,sin(2A- )≤sin
)≤sin =1
=1 ,1]
,1] )-
)- +m,再将M点坐标代入,可得m=
+m,再将M点坐标代入,可得m= ;
; ,所以B=
,所以B= .由此得到函数f(A)=sin(2A-
.由此得到函数f(A)=sin(2A- ),其中A∈(0,
),其中A∈(0, ),再结合正弦函数的图象与性质,可得f(A)的取值范围.
),再结合正弦函数的图象与性质,可得f(A)的取值范围.

科目:高中数学 来源:2012-2013学年河南省驻马店市正阳高中高三(上)第一次素质检测数学试卷(文科)(解析版) 题型:解答题
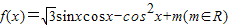 的图象过点M(
的图象过点M(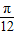 ,0).
,0).查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都电子科大实验中学高三(上)9月周考数学试卷2(理科)(解析版) 题型:解答题
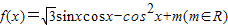 的图象过点M(
的图象过点M(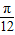 ,0).
,0).查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉市部分学校高三(上)起点调研数学试卷(文科)(解析版) 题型:解答题
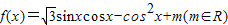 的图象过点M(
的图象过点M(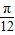 ,0).
,0).查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉市部分学校高三(上)起点调研数学试卷(理科)(解析版) 题型:解答题
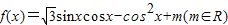 的图象过点M(
的图象过点M(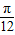 ,0).
,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com