
 :
: 为奇函数,理由如下:
为奇函数,理由如下: 可得函数的定义域为(-∞,0)∪(0,+∞)关于原点对称
可得函数的定义域为(-∞,0)∪(0,+∞)关于原点对称 =
=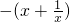 =-f(x)
=-f(x) 为奇函数
为奇函数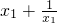 -(
-(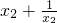 )=
)=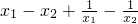 =
=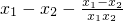 =
=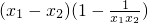 =
=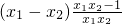


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源:2015届陕西省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题12分)已知函数
 ,
,
(1)判断函数在区间 上的单调性;
上的单调性;
(2)求函数在区间是区间[2,6]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高一上学期期中考试数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)判断函数 的奇偶性;(4分)
的奇偶性;(4分)
(2)若关于 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分)
(3)若 ,记
,记 ,试求函数
,试求函数 在区间
在区间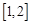 上的最大值.(10分)
上的最大值.(10分)
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省营口市高一上学期期末检测数学试卷 题型:解答题
(本小题满分12分)
已知函数 .
.
(1)判断其奇偶性;
(2)指出该函数在区间(0,1)上的单调性并证明;
(3)利用(1)、(2)的结论,指出该函数在(-1,0)上的增减性.
查看答案和解析>>
科目:高中数学 来源:2010年福建省四地六校高二下学期第二次联考数学(文科)试题 题型:解答题
(本小题满分12分)已知函数 ,
,
(1)判断函数 的奇偶性;(2)求证:方程
的奇偶性;(2)求证:方程 至少有一根在区间
至少有一根在区间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com