
科目:高中数学 来源: 题型:
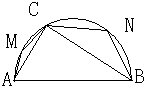 已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.
已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.| S1 | S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
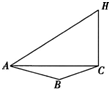 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚| 2 | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:专题七 应用性问题 题型:044
已知大西北的荒漠上的A、B两地相距2 km,现准备在荒漠上围成一片以AB为一条对角线的平行四边形区域建成农艺园.按照规划,围墙的总长为8 km.
(1)农艺园的最大面积能达到多少?
(2)又该荒漠上有一条水沟P恰好经过A,且水沟P与AB成30°角.现欲对整个水沟进行加固改造,但对水沟可能被农艺园围进的部分暂不加固.问水沟暂时不加固的部分有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com