下列四个命题:
①在空间中,存在无数个点到三角形各边的距离相等;
②在空间中,存在无数个点到长方形各边的距离相等;
③在空间中,既存在到长方体各顶点距离相等的点,又存在到它的各个面距离相等的点;
④在空间中,既存在到四面体各顶点距离相等的点,又存在到它的各个面距离相等的点.
其中真命题的序号是________.(写出所有真命题的序号)
①④
分析:对于①,过三角形的内心且垂直于该三角形所在平面的直线上任意一点到该三角形的各边的距离都相等;对于②,假设存在点到长方形的各边的距离相等,则该点到四个顶点的距离相等,该点必在过这个长方形的中心且与这个长方形所在的平面垂直的直线上,由此可知该长方形的长、宽相等,而对于任意的长方形而言其长、宽未必相等;对于③,若存在到长方体的各个面距离相等的点,则该长方体的长、宽、高相等,而对于任意的长方体而言其长、宽、高未必相等;对于④,以四面体的棱为一长方体的侧面的对角线构造长方体,该长方体的体对角线的交点到该四面体的各顶点的距离相等;显然该四面体的内切球的球心到其各面的距离相等,故可判断.
解答:对于①,容易得知,过三角形的内心且垂直于该三角形所在平面的直线上任意一点到该三角形的各边的距离都相等,因此①是真命题.
对于②,假设存在点到长方形的各边的距离相等,则该点到四个顶点的距离相等,该点必在过这个长方形的中心且与这个长方形所在的平面垂直的直线上,由此可知该长方形的长、宽相等,而对于任意的长方形而言其长、宽未必相等,因此②是假命题.
对于③,长方体的体对角线的交点到各顶点的距离相等,若存在到长方体的各个面距离相等的点,则该长方体的长、宽、高相等,而对于任意的长方体而言其长、宽、高未必相等,因此③是假命题.
对于④,以四面体的棱为一长方体的侧面的对角线构造长方体,可知该长方体的体对角线的交点到该四面体的各顶点的距离相等;显然该四面体的内切球的球心到其各面的距离相等,因此④是真命题.
综上所述,其中真命题的序号是①④
故答案为:①④
点评:本题以命题为载体,考查命题的真假判断,解题时需要结合具体的几何体,充分利用几何体的性质一一判断.



 在定义域内是连续函数,数列{an}通项公式为an=
在定义域内是连续函数,数列{an}通项公式为an= ,则数列{an}的所有项之和为1.
,则数列{an}的所有项之和为1.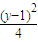 =1有唯一公共点的直线有且只有两条.
=1有唯一公共点的直线有且只有两条. ,
, ,若函数f(x)=
,若函数f(x)= 在区间[-1,1]上是增函数,则实数t的取值范围是(5,+∞);
在区间[-1,1]上是增函数,则实数t的取值范围是(5,+∞);