
【题目】函数f(x)=ax3+bx+ ![]() +2,满足f(﹣3)=﹣2015,则f(3)的值为 .
+2,满足f(﹣3)=﹣2015,则f(3)的值为 .
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设f(x)是[0,1]上的不减函数,即对于0≤x1≤x2≤1有f(x1)≤f(x2),且满足(1)f(0)=0;(2)f( ![]() )=
)= ![]() f(x);(3)f(1﹣x)=1﹣f(x),则f(
f(x);(3)f(1﹣x)=1﹣f(x),则f( ![]() )=( )
)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为椭圆
为椭圆![]() :
: ![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() .
.
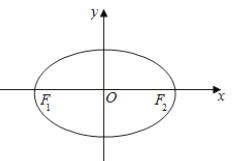
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 的面积为1,
的面积为1, ![]() (
(![]() ,
, ![]() ),当点
),当点![]() 在椭圆
在椭圆![]() 上运动时,试问
上运动时,试问![]() 是否为定值?若是定值,求出这个定值;若不是定值,求出
是否为定值?若是定值,求出这个定值;若不是定值,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x),对任意x1 , x2∈[0,+∞)(x1≠x2),有 ![]() <0,则( )
<0,则( )
A.f(3)<f(﹣2)<f(1)
B.f(1)<f(﹣2)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(1)<f(﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
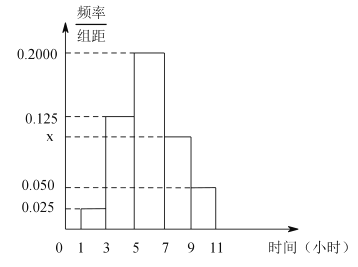
(1)求学习时间在![]() 的学生人数;
的学生人数;
(2)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人学习时间在第四组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段![]() ,
,![]() ,…,
,…,![]() 后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
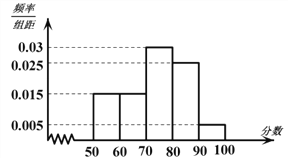
(1)求出这60名学生中化学成绩低于50分的人数;
(2)估计高二年级这次考试化学学科及格率(60分以上为及格);
(3)从化学成绩不及格的学生中随机调查1人,求他的成绩低于50分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时, ![]() (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, ![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com