
 �ڼ�ֵΪa��Ԫ��/1��Ʒ�ɻ��
�ڼ�ֵΪa��Ԫ��/1��Ʒ�ɻ�� ��Ԫ����˰����ڼ�ֵΪb��Ԫ��B��Ʒ�ɻ��
��Ԫ����˰����ڼ�ֵΪb��Ԫ��B��Ʒ�ɻ�� ��Ԫ����˰��.��֪���ҳ����ܼ�ֵΪ100��Ԫ��A��B���ֿڷ�Һ�������ֿڷ�Һ�ij��ڼ�ֵ��������10��Ԫ.
��Ԫ����˰��.��֪���ҳ����ܼ�ֵΪ100��Ԫ��A��B���ֿڷ�Һ�������ֿڷ�Һ�ij��ڼ�ֵ��������10��Ԫ. ʱ�������ƶ�һ������,ʹ������γ���ó���и���ҵ��õ���˰����࣬����������ֵ;����ȷ��0.1���ο����ݣ�
ʱ�������ƶ�һ������,ʹ������γ���ó���и���ҵ��õ���˰����࣬����������ֵ;����ȷ��0.1���ο����ݣ� )
) ����
���� �ı���ʽ.
�ı���ʽ.
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

 �Ƕ�����R�ϵ��溯�����ҵ�
�Ƕ�����R�ϵ��溯�����ҵ� ʱ����ʽ
ʱ����ʽ ������ ��
������ �� ��
��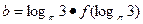 ��
�� ����
���� �Ĵ�С��ϵ��( )
�Ĵ�С��ϵ��( )
A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��������Ȼ��x��y�����㣺
��������Ȼ��x��y�����㣺 ����
����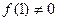 ����
���� ���ڣ� ��
���ڣ� ��| A��1004 | B��1005 | C��2009 | D��2010 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ������{x}��x��[x]����[x]��ʾ������x������������������������ܳ�����СֵΪ
������{x}��x��[x]����[x]��ʾ������x������������������������ܳ�����СֵΪ �鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com