已知定圆C1和两定点M、N，圆心C1不在MN的中垂线上，过MN作圆C2与圆C1交于P、Q两点，求证：PQ必过一定点．
分析：建立直角坐标系，得到圆C1的方程和两定点M、N的坐标，C2在MN的中垂线上，设出C2的坐标（0，k），
写出圆C2的方程，将两圆的方程相减便得到公共弦PQ的方程，再利用直线系过定点得到定点坐标．
解答：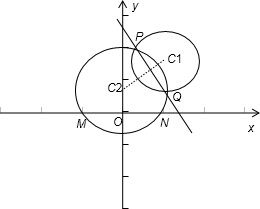
证明：以MN所在的直线为x轴，以其中垂线为 y轴，
建立直角坐标系，如图：设M（-m，0）、N（m，0），C
2（0，k），
设定圆C
1 的方程为 （x-a）
2+（y-b）
2=r
2，
圆C
2的方程为 x
2+（y-k）
2=k
2+m
2，
由题意知，a、b、r、m为定值，k为 参数．
将两圆的方程相减得直线PQ的方程为-2ax+（2k-2b）y+a
2+b
2+m
2-r
2=0，
即2ky+（-2ax-2by+a
2+b
2+m
2-r
2）=0，
由
| | 2ky=0 | | -2ax-2by+a2+b2+m2-r2=0 |
| |
，
得
，
∴直线PQ经过定点（
，0）．
点评：本题考查两圆的位置关系以及直线和圆的位置关系，两圆相交时，将两圆的方程相减即得公共弦所在的直线方程，直线λ（ax+by+c）+（mx+ny+p）=0经过两直线ax+by+c=0与 mx+ny+p=0的交点．
