
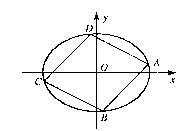
(09年海淀区二模文)(14分)
如图,四边形ABCD的顶点都在椭圆![]() 上,对角线AC、BD互相垂直且平分于原点O.
上,对角线AC、BD互相垂直且平分于原点O.
(1)若点A在第一象限,直线AB的斜率为1,求直线AB的方程;
(2)求四边形ABCD面积的最小值.
解析:(Ⅰ)设A(x1,y1),B(x2,y2),直线AB的方程为![]() 1分
1分
∵四边形ABCD的顶点都在椭圆![]() 上,
上,
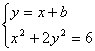 ,∴
,∴![]() ,即
,即![]()
则△![]() 2分
2分
![]() 3分
3分
∴![]()
=![]()
又OA⊥OB,所以![]()
![]() 4分
4分
∴![]()
∴![]() ,
,![]() 5分
5分
∵点A在第一象限∴![]()
所以直线AB的方程为![]() 6分
6分
(Ⅱ)①若直线AB⊥![]() 轴,设其方程为
轴,设其方程为![]() ,此时易知道直线AC、BD的方程分别
,此时易知道直线AC、BD的方程分别
为![]() ,
,![]() ,且四边形ABCD是正方形,
,且四边形ABCD是正方形,
则A(x0,x0),B(x0,―x0),
![]() ,
,
四边形ABCD的面积![]() 8分
8分
②若直线AB的斜率存在,设其方程为![]() ,A(x1,y1),B(x2,y2)
,A(x1,y1),B(x2,y2)
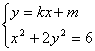 ,∴
,∴![]()
即![]() 9分
9分
则△![]()
=![]()
![]() 10分
10分
∴![]()
=![]()
又![]() 所以
所以
![]()
![]() …………………………11分
…………………………11分
所以|AB|![]()
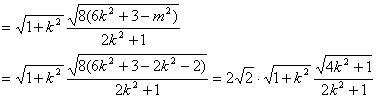
直角三角形OAB斜边AB上的高![]()
所以![]()
 , ……………………13分
, ……………………13分
当且仅当k=0时取得此最小值,此时![]() =8 ……………………14分
=8 ……………………14分


科目:高中数学 来源: 题型:
(09年海淀区二模文)(14分)
数列![]()
(1)当![]() 时,求实数
时,求实数![]() 及a3;
及a3;
(2)是否存在实数![]() ,使得数列{
,使得数列{![]() }为等差数列?若存在,求数列{
}为等差数列?若存在,求数列{![]() }的通项公式,若不存在,说明理由.
}的通项公式,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年海淀区二模文)(14分)
如图,直三棱柱A1B1C1―ABC中,D、E分别是BC、A1B1的中点.
(1)证明:BE//平面A1DC1;
(2)求AB=BC=AA1=1,∠ABC=90°求二面角B1―BC1―E的正切值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com