对于数列{xn},从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列.某同学在学习了这一个概念之后,打算研究首项为正整数a,公比为正整数q(q>0)的无穷等比数列{an}的子数列问题.为此,他任取了其中三项ak,am,an(k<m<n).
(1)若ak,am,an(k<m<n)成等比数列,求k,m,n之间满足的等量关系;
(2)他猜想:“在上述数列{an}中存在一个子数列{bn}是等差数列”,为此,他研究了ak+an与2an的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
(3)他又想:在首项为正整数a,公差为正整数d的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
解:(1)由已知可得:a
k=aq
k-1,a
m=aq
m-1,a
n=aq
n-1,…(1分)
则
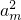
=a
k•a
n,即有(aq
m-1)
2=(aq
k-1)(aq
n-1),….(3分)
2(m-1)=(k-1)+(n-1),化简可得.2m=k+n.…..(4分)
(2)a
k+a
n=aq
k-1+aq
n-1,又2a
m=2aq
m-1,
故 (a
k+a
n)-2a
m=aq
k-1+aq
n-1-2aq
m-1=aq
k-1(1+q
n-k-2q
m-k),…..(6分)
由于k,m,n是正整数,且n>m,则n≥m+1,n-k≥m-k+1,
又q是满足q>1的正整数,则q≥2,
1+q
n-k-2q
m-k≥1+q
m-k+1-2q
m-k=1+q•q
m-k-2q
m-k≥1+2q
m-k-2q
m-k=1>0,
所以,a
k+a
n>2a
m,从而上述猜想不成立.…..(10分)
(3)命题:对于首项为正整数a,公差为正整数d的无穷等差数列{a
n},总可以找到一个无穷子数列{b
n},使得{b
n}是一个等比数列.…(13分)
此命题是真命题,下面我们给出证明.
证法一:只要证明对任意正整数n,b
n=a(1+d)
n,n≥1都在数列{a
n}中.因为b
n=a(1+d)
n=a(1+

d+

d
2+…+

d
n)=a(Md+1),
这里M=

+

d+…+

d
n-1为正整数,所以a(Md+1)=a+aMd是{a
n}中的第aM+1项,证毕.…..(18分)
证法二:首项为a,公差为d( a,d∈N
*)的等差数列为a,a+d,a+2d,…,考虑数列{a
n}中的项:
a+ad,a+(2a+ad)d,a+(3a+3ad+d
2)d,…
依次取数列{b
n}中项b
1=a+ad=a(1+d),b
2=a+(2a+ad)d=a(1+d)
2,b
3=a+(3a+3ad+d
2)d=a(1+d)
3,则由a<2a+ad<3a+3ad+d
2,可知
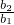
=
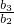
,
并由数学归纳法可知,数列b
n=a(1+d)
n,n≥1为列{a
n}的无穷等比子数列…(18分)
分析:(1)依题意,由
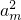
=a
k•a
n,即可求得k,m,n之间满足的等量关系;
(2)利用作差法判断(a
k+a
n)-2a
m的结果是否为0即可判断上述猜想是否正确;
(3)命题:对于首项为正整数a,公差为正整数d的无穷等差数列{a
n},总可以找到一个无穷子数列{b
n},使得{b
n}是一个等比数列,此命题是真命题,;
证法一:利用二项式定理(1+d)
n=(1+

d+

d
2+…+

d
n),即可证明a(Md+1)=a+aMd是{a
n}中的第aM+1项(M=

+

d+…+

d
n-1为正整数);
证法二:先猜想,再利用数学归纳法证明即可.
点评:本题考查等差与等比关系的确定,考查数学归纳法与分析法证明问题的能力,考查考查创新思维与逻辑思维能力及综合运算的能力,属于难题.

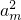 =ak•an,即有(aqm-1)2=(aqk-1)(aqn-1),….(3分)
=ak•an,即有(aqm-1)2=(aqk-1)(aqn-1),….(3分) d+
d+ d2+…+
d2+…+ dn)=a(Md+1),
dn)=a(Md+1), +
+ d+…+
d+…+ dn-1为正整数,所以a(Md+1)=a+aMd是{an}中的第aM+1项,证毕.…..(18分)
dn-1为正整数,所以a(Md+1)=a+aMd是{an}中的第aM+1项,证毕.…..(18分)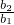 =
=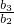 ,
,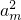 =ak•an,即可求得k,m,n之间满足的等量关系;
=ak•an,即可求得k,m,n之间满足的等量关系; d+
d+ d2+…+
d2+…+ dn),即可证明a(Md+1)=a+aMd是{an}中的第aM+1项(M=
dn),即可证明a(Md+1)=a+aMd是{an}中的第aM+1项(M= +
+ d+…+
d+…+ dn-1为正整数);
dn-1为正整数);

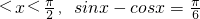 ,存在a,b,c(a,b,c∈N*),使得(b-πc)tan2x-atanx+(b-πc)=0,则a+b+c等于
,存在a,b,c(a,b,c∈N*),使得(b-πc)tan2x-atanx+(b-πc)=0,则a+b+c等于 的右焦点,若过点F且倾斜角为60°的直线与双曲线的右支有两个交点,则该双曲线的离心率e的取值范围是
的右焦点,若过点F且倾斜角为60°的直线与双曲线的右支有两个交点,则该双曲线的离心率e的取值范围是 )
) )
)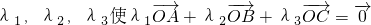 ,设△AOB,△AOC的面积分别为S1、S2,则S1:S2=
,设△AOB,△AOC的面积分别为S1、S2,则S1:S2=