
(本小题12分)设直线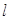 的方程
的方程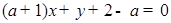 .(1)若
.(1)若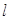 在两坐标轴上截距相等,求
在两坐标轴上截距相等,求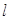 的一般式方程.Z,X
的一般式方程.Z,X
(2)若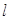 不经过第二象限,求实数
不经过第二象限,求实数 的取值范围.
的取值范围.
科目:高中数学 来源:2011届江西省重点中学联盟高三第一次联考数学文卷 题型:解答题
(本小题满分12分)
在 直三棱柱
直三棱柱 中, AC=4,CB=2,AA1=2
中, AC=4,CB=2,AA1=2 ,E、F分别是
,E、F分别是 的中点。
的中点。
(1)证明:平面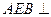 平面
平面 ;
;
(2)证明: 平面ABE;
平面ABE;
(3)设P是BE的中点,求三棱锥 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市高新区高三2月月考理科数学试卷(解析版 题型:解答题
(本小题12分)在直三棱柱(侧棱垂直底面)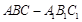 中,
中,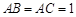 ,
,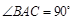 .
.
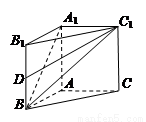
(Ⅰ)若异面直线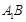 与
与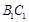 所成的角为
所成的角为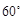 ,求棱柱的高;
,求棱柱的高;
(Ⅱ)设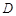 是
是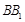 的中点,
的中点,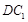 与平面
与平面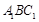 所成的角为
所成的角为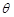 ,当棱柱的高变化时,求
,当棱柱的高变化时,求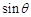 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年丹东市四校协作体高三摸底测试数学理(零诊) 题型:解答题
(本小题满分12分)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,……,依次类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是 .记小球遇到第
.记小球遇到第 行第
行第 个障碍物(从左至右)上顶点的概率为
个障碍物(从左至右)上顶点的概率为 .
.
(Ⅰ)求 ,
, 的值,并猜想
的值,并猜想 的表达式(不必证明);
的表达式(不必证明);
(Ⅱ)已知 ,设小球遇到第6行第
,设小球遇到第6行第 个障碍物(从左至右)上顶点时,
个障碍物(从左至右)上顶点时,
得到的分数为 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省济南市高三12月质量检测数学文卷 题型:解答题
(本小题满分12分)如图,AB为圆O的直
径,点E、F在圆O上,AB∥EF,矩形ABCD
所在的平面和圆O所在的平面垂直,且 .
.
⑴求证: ;
;
⑵设FC的中点为M,求证: ;
;
⑶设平面CBF将几何体分成的两个锥体的体积分别为 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com