
 (a>0,b>0)的左焦点为F,右顶点为A,上顶点为B,若BF⊥BA,则称其为“优美椭圆”,那么“优美椭圆”的离心率为 .
(a>0,b>0)的左焦点为F,右顶点为A,上顶点为B,若BF⊥BA,则称其为“优美椭圆”,那么“优美椭圆”的离心率为 . 科目:高中数学 来源:2009-2010学年吉林省延边州五中高二(下)期中数学试卷(理科)(解析版) 题型:选择题
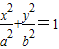 ({a>0,b>0})与抛物线y2=2px(p>0)有相同的焦点,点A是两曲线的交点,且AF⊥x轴,则椭圆的离心率是( )
({a>0,b>0})与抛物线y2=2px(p>0)有相同的焦点,点A是两曲线的交点,且AF⊥x轴,则椭圆的离心率是( )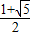
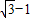
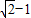
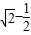
查看答案和解析>>
科目:高中数学 来源:2010年吉林省延边五中高考数学二模试卷(理科)(解析版) 题型:选择题
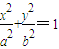 ({a>0,b>0})与抛物线y2=2px(p>0)有相同的焦点,点A是两曲线的交点,且AF⊥x轴,则椭圆的离心率是( )
({a>0,b>0})与抛物线y2=2px(p>0)有相同的焦点,点A是两曲线的交点,且AF⊥x轴,则椭圆的离心率是( )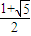
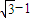
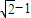
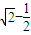
查看答案和解析>>
科目:高中数学 来源:2011年高三数学精品复习15:椭圆及其性质(解析版) 题型:解答题
 (a>0,b>0)的左焦点为F,右顶点为A,上顶点为B,若BF⊥BA,则称其为“优美椭圆”,那么“优美椭圆”的离心率为 .
(a>0,b>0)的左焦点为F,右顶点为A,上顶点为B,若BF⊥BA,则称其为“优美椭圆”,那么“优美椭圆”的离心率为 .查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市重点高中联盟高三联考数学试卷(理科)(解析版) 题型:选择题
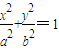 ({a>0,b>0})与抛物线y2=2px(p>0)有相同的焦点,点A是两曲线的交点,且AF⊥x轴,则椭圆的离心率是( )
({a>0,b>0})与抛物线y2=2px(p>0)有相同的焦点,点A是两曲线的交点,且AF⊥x轴,则椭圆的离心率是( )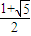


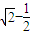
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com