
(1)求证:EF⊥B1C;
(2)求EF与C1G所成角的余弦;
(3)若A为C1G的中点,求FH的长.
思路分析:利用空间向量的基础知识,证明异面直线垂直,求异面直线所成的角及线段的长度.
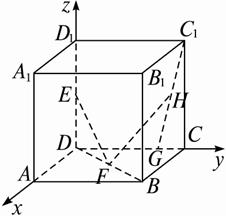
解:如图,建立空间直角坐标系O—xyz,

D为坐标原点O,由已知,有E(0,0,![]() ),F(
),F(![]() ,
,![]() ,0),C(0,1,0),C1(0,1,1),B1(1,1,1),G(0,
,0),C(0,1,0),C1(0,1,1),B1(1,1,1),G(0,![]() ,0).
,0).
(1)∵![]() =(
=(![]() ,
,![]() ,0)-(0,0,
,0)-(0,0,![]() )=(
)=(![]() ,
,![]() ,
,![]() ),
),
![]() =(0,1,0)-(1,1,1)=(-1,0,-1),
=(0,1,0)-(1,1,1)=(-1,0,-1),
∴![]() =
=![]() ×(-1)+
×(-1)+![]() ×0+(
×0+(![]() )×(-1)=0.
)×(-1)=0.
∴![]() .
.
∴EF⊥B1C.
(2)∵![]() =(0,
=(0,![]() ,0)-(0,1,1)=(0,
,0)-(0,1,1)=(0,![]() ,-1),
,-1),
∴|![]() |=
|=![]() .
.
由(1),得|![]() |=
|=![]() .
.
且![]() =
=![]() .
.
所以cos<![]() >=
>=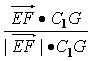 =
=![]() .
.
(3)因为H是C1G的中点,所以H(0,![]() ).
).
又F(![]() 2,0),
2,0),
故|FH|=|![]() |=
|=![]() .
.


科目:高中数学 来源: 题型:
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省南京市金陵中学高三(上)8月月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012年安徽省合肥八中高考数学一模试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com