
如图1在某点B处测得建筑物AE的顶端A的仰角为![]() ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2![]() ,再继续前进10
,再继续前进10![]() m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4![]() ,求
,求![]() 的大小和建筑物AE的高。
的大小和建筑物AE的高。

所求角![]() 为15
为15![]() ,建筑物高度为15m。
,建筑物高度为15m。
(用正弦定理求解)由已知可得在
![]() ACD中, AC=BC=30,
ACD中, AC=BC=30,
AD=DC=10![]() ,
,
![]() ADC =180
ADC =180![]() -4
-4![]() ,
,
![]()
![]() =
=![]() 。
。
∵sin4![]() =2sin2
=2sin2![]() cos2
cos2![]() ,
,![]() cos2
cos2![]() =
=![]() ,得 2
,得 2![]() =30
=30![]() ,
,![]()
![]() =15
=15![]() ,
,
![]() 在Rt
在Rt![]() ADE中,AE=ADsin60
ADE中,AE=ADsin60![]() =15,
=15,
答:所求角![]() 为15
为15![]() ,建筑物高度为15m。
,建筑物高度为15m。
解法二:(设方程来求解)设DE= x,AE=h,
在 Rt![]() ACE中,(10
ACE中,(10![]() + x)
+ x)![]() + h
+ h![]() =30
=30![]() ,
,
在 Rt![]() ADE中,x
ADE中,x![]() +h
+h![]() =(10
=(10![]() )
)![]() ,
,
两式相减,得x=5![]() ,h=15,
,h=15,
![]() 在 Rt
在 Rt![]() ACE中,tan2
ACE中,tan2![]() =
=![]() =
=![]() ,
,
![]() 2
2![]() =30
=30![]() ,
,![]() =15
=15![]() 。
。
答:所求角![]() 为15
为15![]() ,建筑物高度为15m
,建筑物高度为15m
解法三:(用倍角公式求解)设建筑物高为AE=8,由题意,得
![]() BAC=
BAC=![]() ,
, ![]() CAD=2
CAD=2![]() ,
,
AC = BC =30m , AD = CD =10![]() m
m
在Rt![]() ACE中,sin2
ACE中,sin2![]() =
=![]()
在Rt![]() ADE中,sin4
ADE中,sin4![]() =
=![]() ,
,
②![]() ① 得 cos2
① 得 cos2![]() =
=![]() ,2
,2![]() =30
=30![]() ,
,![]() =15
=15![]() ,AE=ADsin60
,AE=ADsin60![]() =15
=15
答:所求角![]() 为15
为15![]() ,建筑物高度为15m
,建筑物高度为15m


科目:高中数学 来源: 题型:
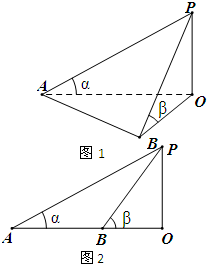 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.| 4 | d |
查看答案和解析>>
科目:高中数学 来源: 题型:
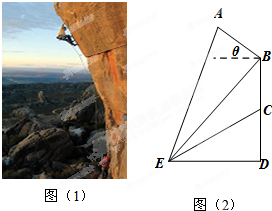 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,画出示意图,如图(2)所示,点A,C分别为两名攀岩者所在位置,点B为山的拐角处,且斜坡AB的坡角为θ,点D为山脚,某人在地面上的点E处测得A,B,C的仰角分别为α,β,γ,ED=a,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,画出示意图,如图(2)所示,点A,C分别为两名攀岩者所在位置,点B为山的拐角处,且斜坡AB的坡角为θ,点D为山脚,某人在地面上的点E处测得A,B,C的仰角分别为α,β,γ,ED=a,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.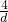 ,旗杆的实际高度为25,试问d为何值时,β-α最大?
,旗杆的实际高度为25,试问d为何值时,β-α最大?查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省常德市芷兰实验学校高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
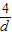 ,旗杆的实际高度为25,试问d为何值时,β-α最大?
,旗杆的实际高度为25,试问d为何值时,β-α最大?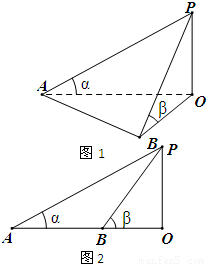
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com