
 表示为若干个正整数(至少3个,且可以相等)之和的形式,若这几个正整数可以按一定顺序构成等差数列,则称这些数为
表示为若干个正整数(至少3个,且可以相等)之和的形式,若这几个正整数可以按一定顺序构成等差数列,则称这些数为 的一个等差分拆.将这些正整数的不同排列视为相同的分拆.如:(1,4,7)与(7,4,1)为12的相同等差分拆.问正整数30的不同等差分拆有 ▲ 个.
的一个等差分拆.将这些正整数的不同排列视为相同的分拆.如:(1,4,7)与(7,4,1)为12的相同等差分拆.问正整数30的不同等差分拆有 ▲ 个.科目:高中数学 来源:不详 题型:填空题
 ,有下列三个命题:①.该二项式展开式中非常数项的系数和是
,有下列三个命题:①.该二项式展开式中非常数项的系数和是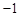 ;②.该二项式展开式中第
;②.该二项式展开式中第 项是
项是 ;③.当
;③.当 时,
时, 除以
除以 的余数是
的余数是 .其中正确命题的序号是 (把你认为正确的序号都填上).
.其中正确命题的序号是 (把你认为正确的序号都填上).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.6 | B.8 | C.12 | D.16 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.21600 | B.10800 | C.7200 | D.5400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com