
为了考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校的高中生中随机地抽取了300名学生进行调查,得到如下列联表:
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
由表中数据计算![]() ,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
约有95%的把握认为“性别与是否喜欢数学课程之间有关系”。
解:可以有95%的把握认为“高中生的性别与是否喜欢数学课程之间有关系”,作出这种判断的依据是独立性检验的基本思想,具体过程为:
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | a | b | a+b |
| 女 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
分别用a,b,c,d表示喜欢数学的男生数、不喜欢数学的男生数、喜欢数学的女生数、不喜欢数学的女生数。如果性别与是否喜欢数学有关系,则男生中喜欢数学的比例![]() 与女生中喜欢数学的比例
与女生中喜欢数学的比例![]() 应该相差很多,即
应该相差很多,即![]() 应很大,将上式等号右边的式子乘以常数因子
应很大,将上式等号右边的式子乘以常数因子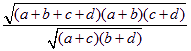 ,然后平方计算得:
,然后平方计算得:![]() ,其中
,其中![]() 因此,
因此,![]() 越大,“性别与是否喜欢数学课程之间有关系”成立的可能性就越大。
越大,“性别与是否喜欢数学课程之间有关系”成立的可能性就越大。
另一方面,假设“性别与是否喜欢数学课程之间没有关系”,由于事件![]() “
“![]() ”的概率为
”的概率为![]() 因此事件A是一个小概率事件。而由样本计算得
因此事件A是一个小概率事件。而由样本计算得![]() ,这表明小概率事件A发生了,由此我们可以断定“性别与是否喜欢数学之间有关系”成立,并且这种判断出错的可能性为5%,约有95%的把握认为“性别与是否喜欢数学课程之间有关系”。
,这表明小概率事件A发生了,由此我们可以断定“性别与是否喜欢数学之间有关系”成立,并且这种判断出错的可能性为5%,约有95%的把握认为“性别与是否喜欢数学课程之间有关系”。


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源:导学大课堂选修数学2-3苏教版 苏教版 题型:013
为了考察高中生的性别与是否喜欢数学课程之间的关系,在某校高中生中随机抽取了300名学生,得到如下列联表:
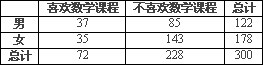
你认为性别与是否喜欢数学课程之间有关系的把握有
0
95%
99%
100%
查看答案和解析>>
科目:高中数学 来源: 题型:
| 喜欢数学课程 | 不喜欢数学课程 | 总计 |
男 | 37 | 85 | 122 |
女 | 35 | 143 | 178 |
总计 | 72 | 228 | 300 |
你认为性别与是否喜欢数学课程之间有关系的把握有( )
A.0 B.95% C.99% D.100%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com