分析:(I)由b
1=1,b
n+1=2b
n+1,分别令n=1和n=2,先求出b
2和b
3,再由b
n+1=2b
n+1,利用构造法求出{b
n}的通项公式.
(II)先证明
=
(n≥2,n∈N
*),由该结论得
| n |
 |
| k=1 |
(1+)=(1+)(1+)…(1+))=2(
+
+…+
+
),再由
+
+…+
+
=1+
+…+
,利用放缩法即可证明结论;
解答:(Ⅰ)解:∵b
1=1,b
n+1=2b
n+1,
∴b
2=2×1+1=3,b
3=2×3+1=7,b
4=2×7+1=15,
∵b
n+1=2b
n+1,∴b
n+1+1=2(b
n+1),
所以{b
n+1}为公比为2的等比数列,首项为2,
∴b
n+1=(b
1+1)•2
n-1=2•2
n-1=2
n,
∴b
n=2
n-1.
(II)证明:a
1=1,a
n=b
n(
++…+)(n≥2且n∈N
*),
∴
=
+
+…+
,
=
+
+…+
+
,
∴
-
=
,∴
=
,
∴
=
(n≥2且n∈N
*).
所以
| n |
 |
| k=1 |
(1+)=(1+)(1+)…(1+))
=
×
××…×
=
×××…×
•an+1=
×
××…×
•a
n+1=
×
•a
n+1=2•
=2(
+
+…+
+
),
而
+
+…+
+
=1+
+…+
,
当k≥2时,
=
<
=2(
-),
∴1+
+…+
=1+2[(
-
)+(
-
)+…+(
-
)
=1+2(
-
)<
<
.
点评:本题考查数列的通项公式的求法,考查不等式的证明,考查数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.







 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案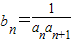 求数列{bn}的前n项和Sn.
求数列{bn}的前n项和Sn.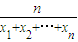 (n∈N*).已知数列{an}前n项的“倒平均数”为
(n∈N*).已知数列{an}前n项的“倒平均数”为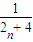 ,记cn=
,记cn= (n∈N*).
(n∈N*).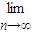 Tn.
Tn.