练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    数集M={x|-3＜x≤5}，N={x|a+1≤x＜4a+1}，若N⊆M，则实数a的取值范围是（　　）
    分析：利用条件N⊆M，建立a的不等式关系即可求解．
    解答：解：若N=∅，即a+1≥4a+1，即a≤0时，满足N⊆M．
    若N≠∅，即a+1＜4a+1，即a＞0时，
    要使N⊆M，
    则满足
    a＞0
    a+1＞-3
    4a+1≤5
    ，即
    a＞0
    a＞-4
    a≤1
    ，解得0＜a≤1，
    综上：a≤1．
    故选：D
    点评：本题主要考查集合关系的应用，考查分类讨论的思想，利用数轴是解决此类问题的基本方法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2009•上海模拟）在解决问题：“证明数集A={x|2＜x≤3}没有最小数”时，可用反证法证明．假设a（2＜a≤3）是A中的最小数，则取a′=
    a+2
    2
    ，可得：2=
    2+2
    2
    ＜a′=
    a+2
    2
    ＜
    a+a
    2
    =a≤3    ，与假设中“a是A中的最小数”矛盾！那么对于问题：“证明数集B={x|x=
    n
    m
    ，m，n∈N*，并且n＜m}    没有最大数”，也可以用反证法证明．我们可以假设x=
    n0
    m0
    是B中的最大数，则可以找到x'=
    n0+1
    m0+1
    n0+1
    m0+1
    （用m0，n0表示），由此可知x'∈B，x'＞x，这与假设矛盾！所以数集B没有最大数．

    查看答案和解析>>

    科目：高中数学 来源：上海模拟 题型：填空题

    在解决问题：“证明数集A={x|2＜x≤3}没有最小数”时，可用反证法证明．假设a（2＜a≤3）是A中的最小数，则取a′=
    a+2
    2
    ，可得：2=
    2+2
    2
    ＜a′=
    a+2
    2
    ＜
    a+a
    2
    =a≤3    ，与假设中“a是A中的最小数”矛盾！那么对于问题：“证明数集B={x|x=
    n
    m
    ，m，n∈N*，并且n＜m}    没有最大数”，也可以用反证法证明．我们可以假设x=
    n0
    m0
    是B中的最大数，则可以找到x'=______（用m0，n0表示），由此可知x'∈B，x'＞x，这与假设矛盾！所以数集B没有最大数．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年上海市十校高三（下）联考数学试卷（理科）（解析版） 题型：解答题

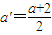    在解决问题：“证明数集A={x|2＜x≤3}没有最小数”时，可用反证法证明．假设a（2＜a≤3）是A中的最小数，则取，可得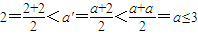：，与假设中“a是A中的最小数”矛盾！那么对于问题：“证明数集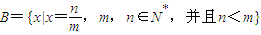没有最大数”，也可以用反证法证明．我们可以假设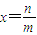是B中的最大数，则可以找到x'=    （用m，n表示），由此可知x'∈B，x'＞x，这与假设矛盾！所以数集B没有最大数．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年上海市十校高三（下）联考数学试卷（文科）（解析版） 题型：解答题

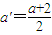    在解决问题：“证明数集A={x|2＜x≤3}没有最小数”时，可用反证法证明．假设a（2＜a≤3）是A中的最小数，则取，可得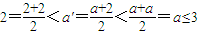：，与假设中“a是A中的最小数”矛盾！那么对于问题：“证明数集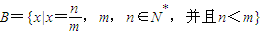没有最大数”，也可以用反证法证明．我们可以假设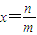是B中的最大数，则可以找到x'=    （用m，n表示），由此可知x'∈B，x'＞x，这与假设矛盾！所以数集B没有最大数．

    查看答案和解析>>

    同步练习册答案