
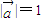 ,
,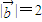 ,且
,且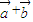 与
与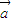 垂直,则向量
垂直,则向量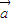 与
与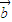 的夹角大小为 .
的夹角大小为 .  暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三压轴文科数学试卷(解析版) 题型:填空题
下面给出的四个命题中:
①以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为 ;
;
②若 ,则直线
,则直线 与直线
与直线 相互垂直;
相互垂直;
③命题 “ ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”;
④将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象。
的图象。
其中是真命题的有 (将你认为正确的序号都填上)。
查看答案和解析>>
科目:高中数学 来源:2012年山东省济南市高考数学三模试卷(文科)(解析版) 题型:填空题
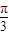 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x-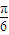 )的图象.
)的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com