已知关于x的不等式k4x-2x+1+6k<0,
(1)若不等式的解集为(1,log23),求实数k的值;
(2)若不等式对一切x∈(1,log23)都成立,求实数k的取值范围;
(3)若不等式的解集为(1,log23)的子集,求实数k的取值范围.
解:(1)关于x的不等式k4
x-2
x+1+6k<0可以化为k(2
x)
2-2×2
x+6k<0,
令2
x=t,∵1<x<log
23,∴2<t<3,则不等式可化为kt
2-2t+6k<0,
∵关于x的不等式k4
x-2
x+1+6k<0的解集为(1,log
23),
∴(2,3)是不等式kt
2-2t+6k<0的解集,
∴2,3是方程kt
2-2t+6k=0的两个实数根,且k<0.
解得
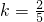
;
(2)∵不等式对一切x∈(1,log
23)都成立,
由(1)可知:即对于2<t<3,不等式kt
2-2t+6k<0恒成立,
等价于:
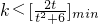
,t∈(2,3).
令
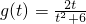
,t∈(2,3).
则
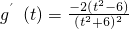
,令g
′(t)=0,解得
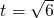
,
当
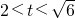
时,g
′(t)>0,函数g(t)在
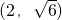
上单调递增;
当
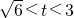
时,g
′(t)<0,函数g(t)在

上单调递减;
而函数g(t)在t=2,3处有意义,且g(2)=

,g(3)=

.
故
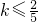
;
(3)因为不等式的解集为(1,log
23)的子集,
由(1)可知:即对于2<t<3,不等式kt
2-2t+6k<0的解集A⊆(2,3),
令f(t)=kt
2-2t+6k,△=4-24k
2,
则
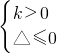
,或
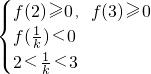
解得
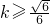
或
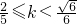
,
即
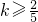
.
分析:(1)通过换元,利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可求出;
(2)把此问题可以转化为恒成立问题解决即可;
(3)把问题转化为利用二次函数的图象与性质研究一元二次不等式的解集即可解决.
点评:熟练掌握一元二次不等式的解法及“三个二次”之间的关系是解题的关键.

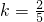 ;
;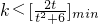 ,t∈(2,3).
,t∈(2,3).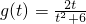 ,t∈(2,3).
,t∈(2,3).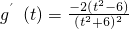 ,令g′(t)=0,解得
,令g′(t)=0,解得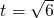 ,
,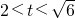 时,g′(t)>0,函数g(t)在
时,g′(t)>0,函数g(t)在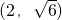 上单调递增;
上单调递增;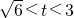 时,g′(t)<0,函数g(t)在
时,g′(t)<0,函数g(t)在 上单调递减;
上单调递减; ,g(3)=
,g(3)= .
.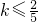 ;
;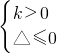 ,或
,或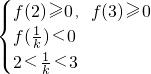
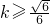 或
或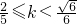 ,
,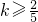 .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案