解:(1)令m=1,n=0,得f(1)=f(1)•f(0)
又当x>0时,0<f(x)<1,所以f(0)=1
设x<0,则-x>0
令m=x,n=-x,则f(0)=f(x)•f(-x)
所以f(x)•f(-x)=1
又0<f(-x)<1,所以f(x)=
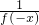
>1
(2)设x
1、x
2∈R,且x
1<x
2,则x
2-x
1>0
所以0<f(x
2-x
1)<1,从而f(x
2)=f(x
2-x
1+x
1)=f(x
2-x
1)•f(x
1),
又由已知条件及(1)的结论知f(x)>0恒成立
所以

=f(x
2-x
1),所以0<

<1,
所以f(x
2)<f(x
1),故f(x)在R上是单调递减的.
由f(x
2)•f(y
2)>f(1)得:f(x
2+y
2)>f(1),
因为f(x)在R上单调递减,所以x
2+y
2<1,即A表示圆x
2+y
2=1的内部,
由f(ax-y+2)=1=f(0)得:ax-y+2=0
所以B表示直线ax-y+2=0,
所以A∩B=∅,所以直线与圆相切或相离,即

≥1
解得:-

≤a≤

.
分析:(1)令m=1,n=0,可求得f(1)=f(1)•f(0),依题意,当x>0时,0<f(x)<1即可证得f(0)=1,再令m=x,n=-x,结合当x<0时,f(x)>1即可证得当x<0时,f(x)>1;
(2)先利用函数的单调性的定义判断函数f(x)在R上是单调递减的,再理清集合A与集合B表示的点集,最后由A∩B=∅,利用图形间的几何意义可求a的取值范围.
点评:本题考查抽象函数及其应用,突出考查函数的单调性的定义判断及集合A与集合B表示的点集的几何意义,考查直线与圆的位置关系,考查转化思想与运算能力,属于难题.

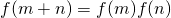 ,且当x>0时,0<f(x)<1.
,且当x>0时,0<f(x)<1.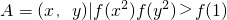 ,B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=∅,求a的取值范围.
,B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=∅,求a的取值范围.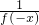 >1
>1 =f(x2-x1),所以0<
=f(x2-x1),所以0< <1,
<1, ≥1
≥1 ≤a≤
≤a≤ .
.

 快捷英语周周练系列答案
快捷英语周周练系列答案