
【题目】若实数x,y满足不等式组  ,目标函数z=kx﹣y的最大值为12,最小值为0,则实数k= .
,目标函数z=kx﹣y的最大值为12,最小值为0,则实数k= .
【答案】3
【解析】解:实数x,y满足不等式组 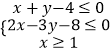 的可行域如图:得:A(1,3),B(1,﹣2),C(4,0). ①当k=0时,目标函数z=kx﹣y的最大值为12,最小值为0,不满足题意.
的可行域如图:得:A(1,3),B(1,﹣2),C(4,0). ①当k=0时,目标函数z=kx﹣y的最大值为12,最小值为0,不满足题意.
②当k>0时,目标函数z=kx﹣y的最大值为12,最小值为0,当直线z=kx﹣y过C(4,0)时,Z取得最大值12.
当直线z=kx﹣y过A(3,1)时,Z取得最小值0.
可得k=3,满足题意.
③当k<0时,目标函数z=kx﹣y的最大值为12,最小值为0,当直线z=kx﹣y过C(4,0)时,Z取得最大值12.可得k=﹣3,
当直线z=kx﹣y过,B(1,﹣2)时,Z取得最小值0.可得k=﹣2,
无解.
综上k=3
所以答案是:3.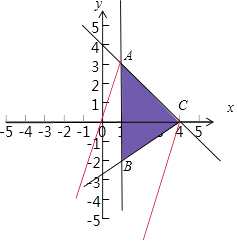


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( ) 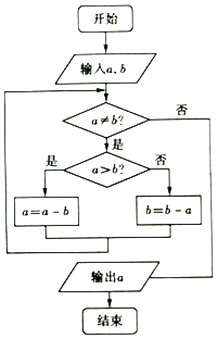
A.14
B.7
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a,b∈R,且a≠0,e为自然对数的底数).
(a,b∈R,且a≠0,e为自然对数的底数).
(I)若曲线f(x)在点(e,f(e))处的切线斜率为0,且f(x)有极小值,求实数a的取值范围.
(II)(i)当 a=b=l 时,证明:xf(x)+2<0;
(ii)当 a=1,b=﹣1 时,若不等式:xf(x)>e+m(x﹣1)在区间(1,+∞)内恒成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)满足f′(x)+2f(x)= ![]() ,且f(1)=
,且f(1)= ![]() ,则不等式f(lnx)>f(3)的解集为( )
,则不等式f(lnx)>f(3)的解集为( )
A.(﹣∞,e3)
B.(0,e3)
C.(1,e3)
D.(e3 , +∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ﹣4cosθ=0.
(t为参数),若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ﹣4cosθ=0.
(1)求直线l与曲线C的普通方程;
(2)已知直线l与曲线C交于A,B两点,设M(2,0),求| ![]() |的值.
|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已成椭圆C: ![]() =1(a>b>0)的左右顶点分别为A1、A2 , 上下顶点分别为B2/B1 , 左右焦点分别为F1、F2 , 其中长轴长为4,且圆O:x2+y2=
=1(a>b>0)的左右顶点分别为A1、A2 , 上下顶点分别为B2/B1 , 左右焦点分别为F1、F2 , 其中长轴长为4,且圆O:x2+y2= ![]() 为菱形A1B1A2B2的内切圆.
为菱形A1B1A2B2的内切圆.
(1)求椭圆C的方程;
(2)点N(n,0)为x轴正半轴上一点,过点N作椭圆C的切线l,记右焦点F2在l上的射影为H,若△F1HN的面积不小于 ![]() n2 , 求n的取值范围.
n2 , 求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:若定义域为R的函数f(x)不是偶函数,则x∈R,f(﹣x)≠f(x).命题q:f(x)=x|x|在(﹣∞,0)上是减函数,在(0,+∞)上是增函数.则下列判断错误的是( )
A.p为假
B.¬q为真
C.p∨q为真
D.p∧q为假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,E,F分别是AB,CD1的中点,AA1=AD=1,AB=2. 
(1)求证:EF∥平面BCC1B1;
(2)求证:平面CD1E⊥平面D1DE;
(3)在线段CD1上是否存在一点Q,使得二面角Q﹣DE﹣D1为45°,若存在,求 ![]() 的值,不存在,说明理由.
的值,不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com