
【题目】函数f(x)=xex .
(1)求f(x)的极值;
(2)k×f(x)≥ ![]() x2+x在[﹣1,+∞)上恒成立,求k值的集合.
x2+x在[﹣1,+∞)上恒成立,求k值的集合.
【答案】
(1)解:f′(x)=ex(x+1),
令f′(x)>0,解得:x>﹣1,
令f′(x)<0,解得:x<﹣1,
∴f(x)在(﹣∞,﹣1)递减,在(﹣1,+∞)递增,
∴f(x)在极小值是f(﹣1)=﹣ ![]() ,无极大值
,无极大值
(2)解:x>0时,k≥ ![]() ,
,
令φ(x)= ![]() ,则φ′(x)=
,则φ′(x)= ![]()
![]() <0,
<0,
φ(x)在(0,+∞)递减,
故φ(x)≤φ(0)=1,即k≥1;
﹣1≤x<0时,k≤ ![]() ,
,
φ′(x)= ![]() <0,
<0,
故φ(x)在[﹣1,0]递减,φ(x)≥φ(0)=1,
故k≤1,
综上,k=1,
故k∈{1}
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的最小值即可;(2)分离参数,令φ(x)= ![]() ,根据函数的单调性求出k的值即可.
,根据函数的单调性求出k的值即可.


科目:高中数学 来源: 题型:
【题目】某村投资128万元建起了一处生态采摘园,预计在经营过程中,第一年支出10万元,以后每年支出都比上一年增加4万元,从第一年起每年的销售收入都为76万元.设y表示前n(n∈N*)年的纯利润总和(利润总和=经营总收入﹣经营总支出﹣投资).
(1)该生态园从第几年开始盈利?
(2)该生态园前几年的年平均利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+ ![]() x2在x=﹣1处取得极大值,记g(x)=
x2在x=﹣1处取得极大值,记g(x)= ![]() .程序框图如图所示,若输出的结果S>
.程序框图如图所示,若输出的结果S> ![]() ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( ) 
A.n≤2014?
B.n≤2015?
C.n>2014?
D.n>2015?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为丰富中学生的课余生活,增进中学生之间的交往与学习,某市甲乙两所中学举办一次中学生围棋擂台赛.比赛规则如下,双方各出3名队员并预先排定好出场顺序,双方的第一号选手首先对垒,双方的胜者留下进行下一局比赛,负者被淘汰出局,由第二号选手挑战上一局获胜的选手,依此类推,直到一方的队员全部被淘汰,另一方算获胜.假若双方队员的实力旗鼓相当(即取胜对手的概率彼此相等) (Ⅰ)在已知乙队先胜一局的情况下,求甲队获胜的概率.
(Ⅱ)记双方结束比赛的局数为ξ,求ξ的分布列并求其数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为D,若对于a,b,c∈D,f(a),f(b),f(c)分别为某个三角形的三边长,则称f(x)为“三角形函数”.给出下列四个函数: ①f(x)=lg(x+1)(x>0);
②f(x)=4﹣cosx;
③ ![]() ;
;
④ ![]()
其中为“三角形函数”的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴的正半轴上,过点F的直线l与抛物线C相交于A、B两点,且满足 ![]() .
.
(1)求抛物线C的标准方程;
(2)若点M在抛物线C的准线上运动,其纵坐标的取值范围是[﹣1,1],且 ![]() ,点N是以线段AB为直径的圆与抛物线C的准线的一个公共点,求点N的纵坐标的取值范围.
,点N是以线段AB为直径的圆与抛物线C的准线的一个公共点,求点N的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= ![]() PD.
PD.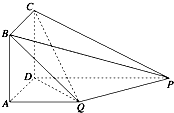
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q﹣BP﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com