
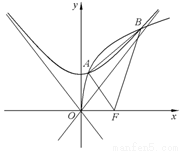
设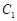 是以
是以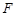 为焦点的抛物线
为焦点的抛物线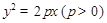 ,
, 是以直线
是以直线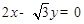 与
与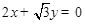 为渐近线,以
为渐近线,以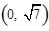 为一个焦点的双曲线.
为一个焦点的双曲线.
(1)求双曲线 的标准方程;
的标准方程;
(2)若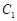 与
与 在第一象限内有两个公共点
在第一象限内有两个公共点 和
和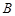 ,求
,求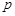 的取值范围,并求
的取值范围,并求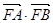 的最大值;
的最大值;
(3)若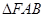 的面积
的面积 满足
满足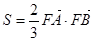 ,求
,求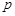 的值.
的值.
(1)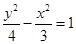 (2)当且仅当
(2)当且仅当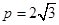 时
时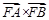 的最大值为9(3)
的最大值为9(3)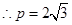
【解析】(1)注意焦点在y轴上,并且由渐近线方程可得到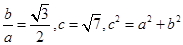 ,可求出a,b值,写出双曲线的标准方程.
,可求出a,b值,写出双曲线的标准方程.
(II)将抛物线方程与双曲线方程联立消y之后得到关于x的一元二次方程,然后利用此方程有两个不同的正实根,确定出p的取值范围,然后再把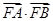 用坐标表示出来,再利用韦达定理转化为关于p的函数,再研究其最值即可.
用坐标表示出来,再利用韦达定理转化为关于p的函数,再研究其最值即可.
(III)先把面积表示出来,在(II)的基础上,先求出|AB|的长度,再根据点到直线的距离公式求出高,最后把S表示成关于p的函数,根据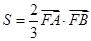 可建立p的方程,解出p的值.
可建立p的方程,解出p的值.
(1)设双曲线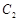 的标准方程为:
的标准方程为: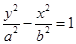 则据题得:
则据题得: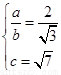
又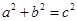
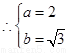
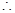 双曲线
双曲线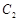 的标准方程为:
的标准方程为: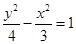
(2)将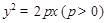 代入到
代入到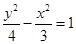 中并整理得:
中并整理得: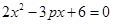
设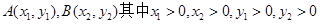 则
则
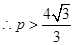 又
又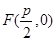
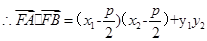
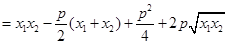
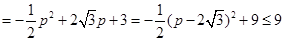
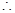 当且仅当
当且仅当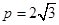 时
时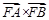 的最大值为9
的最大值为9
(3)直线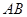 的方程为:
的方程为: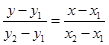 即
即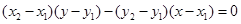
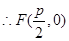 到直线
到直线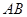 的距离为:
的距离为: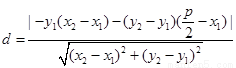

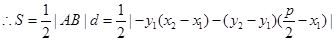
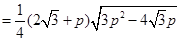
又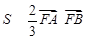
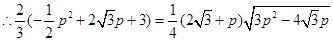
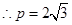


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012学年山西省高三第一次模拟试题理科数学试卷(解析版) 题型:解答题
设 是以
是以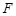 为焦点的抛物线
为焦点的抛物线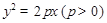 ,
,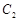 是以直线
是以直线 与
与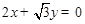 为渐近线,以
为渐近线,以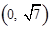 为一个焦点的双曲线.
为一个焦点的双曲线.
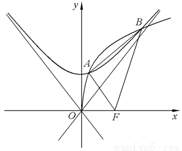
(1)求双曲线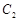 的标准方程;
的标准方程;
(2)若 与
与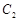 在第一象限内有两个公共点
在第一象限内有两个公共点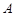 和
和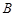 ,求
,求 的取值范围,并求
的取值范围,并求 的最大值;
的最大值;
(3)若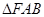 的面积
的面积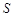 满足
满足 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011年江西省高二第四次月考数学理卷 题型:解答题
设椭圆 的左,右焦点为
的左,右焦点为 ,
, ,(1,
,(1, )为椭圆上一点,椭圆的
)为椭圆上一点,椭圆的
长半轴长等于焦距,曲线C是以坐标原点为顶点,以 为焦点的抛物线,自
为焦点的抛物线,自 引直线交曲线C于P,Q两个不同的交点,点P关于
引直线交曲线C于P,Q两个不同的交点,点P关于 轴的对称点记为M,设
轴的对称点记为M,设 .
.
(1)求椭圆方程和抛物线方程;
(2)证明: ;
;
(3)若 求|PQ|的取值范围
求|PQ|的取值范围
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市七校高三(下)联考数学试卷(理科)(解析版) 题型:解答题
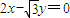 与
与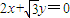 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.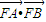 的最大值;
的最大值; 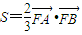 ,求p的值.
,求p的值.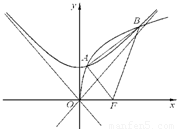
查看答案和解析>>
科目:高中数学 来源:2011-2012学年贵州省贵阳市重点中学高三(下)七校联考数学试卷(理科)(解析版) 题型:解答题
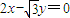 与
与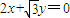 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线. 的最大值;
的最大值; 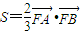 ,求p的值.
,求p的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com