
等比数列 中
中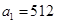 ,公比
,公比 ,用
,用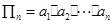 表示它的前n项之积,则
表示它的前n项之积,则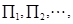 中最大的是( )
中最大的是( )
A.  B.
B. C.
C.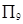 D.
D.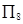
C
【解析】
试题分析:∵在等比数列{an}中,a1=512,公比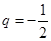 ,∴an=512•(
,∴an=512•(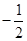 )n-1,则|an|=512•(
)n-1,则|an|=512•(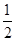 )n-1.
)n-1.
令|an|=1,得n=10,∴|Πn|最大值在n=10之时取到,因为n>10时,|an|<1,n越大,会使|Πn|越小.
∴n为偶数时,an为负,n为奇数时,an为正.
∵Πn=a1a2…an,∴Πn 的最大值要么是a10,要么是a9.
∵Π10 中有奇数个小于零的项,即a2,a4,a6,a8,a10,则Π10<0,
而 Π9 中有偶数个项小于零,即a2,a4,a6,a8,故 Π9 最大,
故答案为 Π9.选C。
考点:本题主要考查等比数列的概念及通项公式。
点评:新定义问题,解题时要认真审题,仔细解答,注意合理地进行转化,属于中档题。


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| Tn |
| ak |
| SnTn |
| Tn(1)+Tn(2)+…+Tn(n) |
| a12 |
| 2-q-q-1 |
| q-qn+1+1-q1-n |
| 1-q |
| a12 |
| 2-q-q-1 |
| q-qn+1+1-q1-n |
| 1-q |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 用Sm表示S2m | S2m=2Sm+m2d | ||||
| 用Sm1、Sm2表示Sm1+m2 | Sm1+m2= Sm1+Sm2+m1m2d Sm1+Sm2+m1m2d ① | ||||
| 用Sm表示Snm | Snm= nSm+
nSm+ ②
|
查看答案和解析>>
科目:高中数学 来源:广州省2009-2010学年高二学科竞赛(数学理) 题型:解答题
(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表, 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为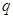 ,若已知
,若已知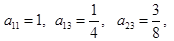
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
(1)求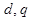 的值;
的值;
(2)求用 表示
表示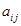 的代数式;
的代数式;
(3)设表中对角线上的数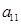 ,
,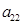 ,
,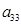 ,……,
,……, 组成一列数列,设Tn=
组成一列数列,设Tn=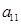 +
+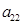 +
+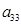 +……+
+……+ 求使不等式
求使不等式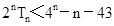 成立的最小正整数n.
成立的最小正整数n.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com