
【题目】在四边形ABCD中(如图①),AB∥CD,AB⊥BC,G为AD上一点,且AB=AG=1,GD=CD=2,M为GC的中点,点P为边BC上的点,且满足BP=2PC.现沿GC折叠使平面GCD⊥平面ABCG(如图②). 
(1)求证:平面BGD⊥平面GCD:
(2)求直线PM与平面BGD所成角的正弦值.
【答案】
(1)证明:在直角梯形ABCD中,AB=AG=1,GD=CD=2,BC=2 ![]() ,cosD=
,cosD= ![]() ,
,
∴GC= ![]() =
= ![]() ,BG=
,BG= ![]() ,
,
∴BG2+GC2=BC2,∴BG⊥GC,
∵平面GCD⊥平面ABCG,平面GCD∩平面ABCG=GC,
∴BG⊥平面GCD,
∵BG平面GCD,
∴平面BGD⊥平面GCD
(2)解:取BP的中点H,连接GH,则GH∥MP,作HQ⊥平面BGD,连接GQ,则∠HGQ为直线GH与平面BGD所成的角,即直线PM与平面BGD所成角.
由(1),作CN⊥GD,则CN⊥平面BGD,
∵HQ⊥平面BGD,
∴HQ∥GN,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴HQ= ![]() CN.
CN.
△DGC中,GC= ![]() ,DM=
,DM= ![]() ,
,
由GDCN=GCDM,得CN= ![]() ,
,
∴HQ= ![]() ,
,
∵直角梯形ABCD中,GH= ![]() ,∴sin∠HGQ=
,∴sin∠HGQ= ![]() =
= ![]() ,
,
∴直线PM与平面BGD所成角的正弦值为 ![]() .
.
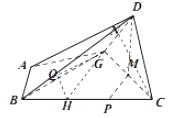
【解析】(1)利用勾股定理,证明BG⊥GC,根据平面与平面垂直的性质,证明BG⊥平面GCD,即可证明平面BGD⊥平面GCD:(2)取BP的中点H,连接GH,则GH∥MP,作HQ⊥平面BGD,连接GQ,则∠HGQ为直线GH与平面BGD所成的角,即直线PM与平面BGD所成角.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则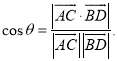 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}和{bn}满足:对任意n∈N* , an , bn , an+1成等差数列,bn , an+1 , bn+1成等比数列,且a1=1,b1=2,a2=3.
(Ⅰ)证明数列{ ![]() }是等差数列;
}是等差数列;
(Ⅱ)求数列{ ![]() }前n项的和.
}前n项的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1: ![]() (φ为参数,实数a>0),曲线C2:
(φ为参数,实数a>0),曲线C2: ![]() (φ为参数,实数b>0).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α(ρ≥0,0≤α≤
(φ为参数,实数b>0).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α(ρ≥0,0≤α≤ ![]() )与C1交于O、A两点,与C2交于O、B两点.当α=0时,|OA|=1;当α=
)与C1交于O、A两点,与C2交于O、B两点.当α=0时,|OA|=1;当α= ![]() 时,|OB|=2.
时,|OB|=2.
(Ⅰ)求a,b的值;
(Ⅱ)求2|OA|2+|OA||OB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市居民的生活成本,甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),甲、乙、丙所调查数据的标准差分别为x1 , x2 , x3 , 则它们的大小关系为( ) 
A.s1>s2>s3
B.s1>s3>s2
C.s3>s2>s1
D.s3>s1>s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)是定义在R上的偶函数,f(x+1)为奇函数,f(0)=0,当x∈(0,1]时,f(x)=log2x,则在区间(8,9)内满足方f(x)程f(x)+2=f( ![]() )的实数x为 ( )
)的实数x为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+2,g(x)=x2﹣mx.
(Ⅰ)求函数f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ)若方程f(x)+g(x)=0有两个不同的实数根,求证:f(1)+g(1)<0;
(Ⅲ)若存在x0∈[ ![]() ,e]使得mf′(x)+g(x)≥2x+m成立,求实数m的取值范围.
,e]使得mf′(x)+g(x)≥2x+m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.
(Ⅰ)若 AF=1,求证:CE∥平面 BDF;
(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2sin
=(2sin ![]() ,2sin
,2sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣
,﹣ ![]() sin
sin ![]() ). (Ⅰ)求函数f(x)=
). (Ⅰ)求函数f(x)= ![]()
![]() +
+ ![]() 的最小正周期;
的最小正周期;
(Ⅱ)若β= ![]() ,g(β)=tan2α,α≠
,g(β)=tan2α,α≠ ![]() +
+ ![]() 且α≠
且α≠ ![]() +kπ(k∈Z),数列{an}满足a1=
+kπ(k∈Z),数列{an}满足a1= ![]() ,an+12=
,an+12= ![]() ang(an)(n≤16且n∈N*),令bn=
ang(an)(n≤16且n∈N*),令bn= ![]() ,求数列{bn}的通项公式及前n项和Sn .
,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com