求函数y=

在区间[2,6]上的最大值和最小值。
解:设x
1、x
2是区间[2,6]上的任意两个实数,且x
1<x
2,
则f(x
1)-f(x
2)=
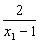
-

=
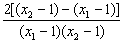
=
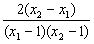
,
由2<x
1<x
2<6,得x
2-x
1>0,(x
1-1)(x
2-1)>0,
于是f(x
1)-f(x
2)>0,即f(x
1)>f(x
2),
所以函数y=

是区间[2,6]上的减函数,
因此,函数y=
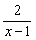
在区间的两个端点上分别取得最大值与最小值,
即当x=2时,y
max=2;当x=6时,y
min=
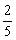
。
练习册系列答案
相关习题
科目:高中数学
来源:2012-2013学年黑龙江省双鸭山市友谊县红兴隆管理局高中高一(上)期中数学试卷(解析版)
题型:解答题
求函数y=
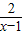
在区间[2,6]上的最大值和最小值.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年黑龙江省双鸭山一中高一(上)期中数学试卷(解析版)
题型:解答题
求函数y=

在区间[2,6]上的最大值和最小值.
查看答案和解析>>
科目:高中数学
来源:《第1章 集合与函数概念》2010年单元测试卷1(大纲版)(解析版)
题型:解答题
求函数y=

在区间[2,6]上的最大值和最小值.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年安徽省高一(上)月考数学试卷(必修1)(解析版)
题型:解答题
求函数y=
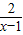
在区间[2,6]上的最大值和最小值.
查看答案和解析>>

 在区间[2,6]上的最大值和最小值。
在区间[2,6]上的最大值和最小值。 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案