Question

已知中心在原点O，焦点F₁、F₂在x轴上的椭圆E经过点C（2，2），且抛物线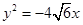的焦点为F₁.

（Ⅰ）求椭圆E的方程；

（Ⅱ）垂直于OC的直线l与椭圆E交于A、B两点，当以AB为直径的圆P与y轴相切时，求直线l的方程和圆P的方程.

 

Answer 1

【答案】

（1）；（2）直线l方程为y=-x－3，圆P的方程为（x+2）²+(y+1)²=4.

【解析】第一问中，利用焦点F₁、F₂在x轴上的椭圆E经过点C（2，2），且抛物线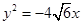的焦点为F₁. ，所以

第二问中，利用依题意，直线OC斜率为1，由此设直线l的方程为y=-x+m代入椭圆E方程，得结合韦达定理进行标示可以得到所求的。

 

解：(Ⅰ)设椭圆E的方程为

①…………………………………………………………………………1分

       

          ②……………………………………………………………………………２分

          ③

由①、②、③得a²=12,b²=6………………………………………………………………3分

所以椭圆E的方程为………………………………………………………4分

(Ⅱ)依题意，直线OC斜率为1，由此设直线l的方程为y=-x+m，………………………5分

 代入椭圆E方程，得………………………………………6分

………………………………7分

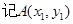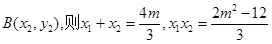、…………………………8分

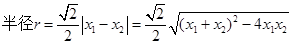………………………………………9分

…………………………………………10分

    当m=3时，直线l方程为y=-x+3，此时，x₁ +x₂=4，圆心为（2，1），半径为2，

圆P的方程为（x-2）²+(y-1)²=4；………………………………………………………11分

同理，当m=－3时，直线l方程为y=-x－3，

圆P的方程为（x+2）²+(y+1)²=4；………………………………………………………12分