
| 10 | 1+2-t+4 |
| 10 |
| 1+2-t+4 |
| u |
| (1+u)(1+2u) |
| 10 |
| 1+2-t+4 |
| 1 |
| 4 |
| 10 |
| 1+2-t0+4 |
| 10 |
| 1+2-t0+5 |
| 10•2-t0+4 |
| (1+2-t0+4)(1+2-t0+5) |
| u |
| (1+u)(1+2u) |
| u |
| 2u2+3u+1 |
| 1 | ||
2u+
|
| 1 | ||||
2
|
| 1 | ||
2
|
| 1 |
| u |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| 5 |
| 3 |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:2013-2014学年上海市徐汇区高三上学期期末考试(一模)理科数学试卷(解析版) 题型:解答题
某种海洋生物身体的长度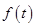 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: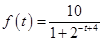 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第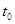 年,该生物长得最快,求
年,该生物长得最快,求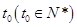 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市徐汇区高三上学期期末考试(一模)文科数学试卷(解析版) 题型:解答题
某种海洋生物身体的长度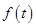 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: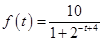 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)该生物出生后第3年和第4年各长了多少米?并据此判断,这2年中哪一年长得更快.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com