练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，动点M到两定点A(－1，0)、B(2，0)构成△MAB，且∠MBA＝2∠MAB，设动点M的轨迹为C．

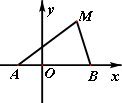
    (Ⅰ)求轨迹C的方程；

    (Ⅱ)设直线y＝－2x＋m与y轴交于点P，与轨迹C相交于点Q、R，且|PQ|＜|PR|，求的取值范围．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

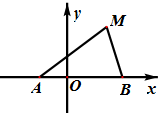    （2012•四川）如图，动点M到两定点A（-1，0）、B（2，0）构成△MAB，且∠MBA=2∠MAB，设动点M的轨迹为C．
    （Ⅰ）求轨迹C的方程；
    （Ⅱ）设直线y=-2x+m与y轴交于点P，与轨迹C相交于点Q、R，且|PQ|＜|PR|，求
    |PR||PQ|
    的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：高考真题 题型：解答题

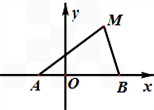
    如图，动点M到两定点A（-1，0）、B（2，0）构成△MAB，且∠MBA=2∠MAB，设动点M的轨迹为C。
    （1）求轨迹C的方程；
    （2）设直线y=-2x+m与y轴交于点P，与轨迹C相交于点Q、R，且|PQ|＜|PR|，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年内蒙古包头33中高二（上）期末数学试卷（理科）（解析版） 题型：解答题

    如图，动点M到两定点A（-1，0）、B（2，0）构成△MAB，且∠MBA=2∠MAB，设动点M的轨迹为C．
    （Ⅰ）求轨迹C的方程；
    （Ⅱ）设直线y=-2x+m与y轴交于点P，与轨迹C相交于点Q、R，且|PQ|＜|PR|，求的取值范围．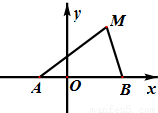

    查看答案和解析>>

    科目：高中数学 来源：2012年四川省高考数学试卷（理科）（解析版） 题型：解答题

    如图，动点M到两定点A（-1，0）、B（2，0）构成△MAB，且∠MBA=2∠MAB，设动点M的轨迹为C．
    （Ⅰ）求轨迹C的方程；
    （Ⅱ）设直线y=-2x+m与y轴交于点P，与轨迹C相交于点Q、R，且|PQ|＜|PR|，求的取值范围．

    查看答案和解析>>

    同步练习册答案