
对于函数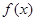 ,若
,若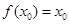 ,则称
,则称 为函数
为函数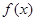 的“不动点”;若
的“不动点”;若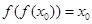 ,则称
,则称 为函数
为函数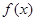 的“稳定点”.如果函数
的“稳定点”.如果函数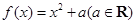 的“稳定点”恰是它的“不动点”,那么实数
的“稳定点”恰是它的“不动点”,那么实数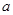 的取值范围是( )
的取值范围是( )
A.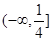 B.
B. C.
C.  D.
D.
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
(本小题满分14分)
对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”,若
的“不动点”,若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源:2012届湖南省涟源一中高三第四次月考理科数学试卷 题型:解答题
对于函数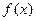 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称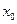 为
为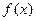 的不动点.如果函数
的不动点.如果函数 有且仅有两个不动点0,2,且
有且仅有两个不动点0,2,且 .
.
(1) 求函数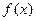 的单调区间;
的单调区间;
(2) 已知数列 各项不为零且不为1,满足
各项不为零且不为1,满足 ,求证:
,求证: ;
;
设 ,
, 为数列
为数列 的前
的前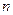 项和,求证:
项和,求证: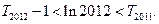
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省四地六高三第三次月考理科数学试卷(解析版) 题型:填空题
对于函数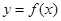 ,若存在区间
,若存在区间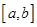 ,当
,当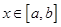 时的值域为
时的值域为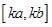
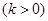 ,则称
,则称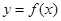 为
为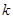 倍值函数.若
倍值函数.若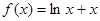 是
是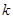 倍值函数,则实数
倍值函数,则实数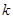 的取值范围是 。
的取值范围是 。
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省瓦房店市五校高二上学期竞赛数学理卷 题型:解答题
.(本小题满分12分)对于函数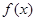 ,若
,若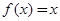 ,则称
,则称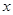 为
为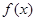 的“不动点”,若
的“不动点”,若 ,则称
,则称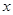 为
为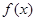 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为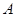 和
和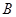 ,即
,即 ,
,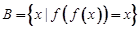 .
.
(1)求证: ;
;
(2)若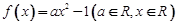 ,且
,且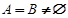 ,求实数
,求实数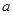 的取值范围;
的取值范围;
(3)若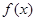 是
是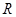 上的单调递增函数,
上的单调递增函数,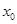 是函数的稳定点,问
是函数的稳定点,问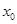 是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com