
 (1-x±
(1-x± ),由定义域知-
),由定义域知- <x<1,由此借助三角函数能求出[9xy]的最大值.
<x<1,由此借助三角函数能求出[9xy]的最大值. (1-x±
(1-x±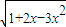 ),由定义域知-
),由定义域知- <x<1,
<x<1, (1-x-
(1-x- ),
), •
• >0,1-x>1+3x,x<0,与x,y同为正数不符,
>0,1-x>1+3x,x<0,与x,y同为正数不符, (1-x+
(1-x+ ),且y>0,x>0,
),且y>0,x>0, -(x-
-(x- )2],
)2], =
= sinα,即x=
sinα,即x= (1+2sinα),其中-
(1+2sinα),其中- ≤α≤
≤α≤ ,
, <α≤
<α≤ ,
, (1-x+
(1-x+ )=
)= (1-sinα+
(1-sinα+ cosα),
cosα), cosα,tanα≠
cosα,tanα≠ ,知α≠
,知α≠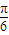 ,
, cosα)=1+sinα+
cosα)=1+sinα+ cosα-2sin2α+2
cosα-2sin2α+2 sinαcosα,
sinαcosα,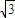 cosα)2=sin2α+2
cosα)2=sin2α+2 sinαcosα+3cos2α=3-2sin2α+2
sinαcosα+3cos2α=3-2sin2α+2 sinαcosα,
sinαcosα,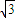 cosα+(sinα+
cosα+(sinα+ cosα)2=(sinα+
cosα)2=(sinα+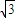 cosα+
cosα+ )2-
)2- ,
, cosα=2sin(α+
cosα=2sin(α+ ),-
),- <α≤
<α≤ ,α≠
,α≠ ,
, <α+
<α+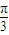 ≤
≤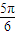 ,但α+
,但α+ ≠
≠ ,
,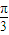 )<2.
)<2. cosα+
cosα+ )2-
)2- <(2+
<(2+ )2-
)2- =4.
=4.

科目:高中数学 来源:2013年江苏省高考数学模拟试卷(十)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com