
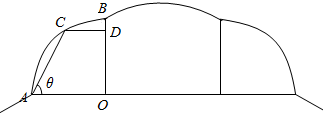
分析 (1)构造辅助线,利用几何关系找出半径与角的关系.
(2)利用函数关系式求出折线ACD最长时θ的值,从而求出点D与点O的位置关系.
解答 解:(1)过点C作CD⊥OA于E,连接OC,得下图: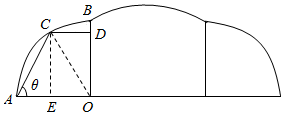
则有:cosθ=$\frac{AE}{AC}$
∴AC=$\frac{AE}{cosθ}$,
∵CD⊥OB,∠AOB=90°,
∴CD平行等于OE
即AC=$\frac{OA-CD}{cosθ}$,
∵∠OAC=∠ACO=θ,
∴∠AOC=∠OCD=π-2θ,
∴CD=OC•cos(π-2θ),
即f(θ)=4cos(π-2θ)+$\frac{4-4cos(π-2θ)}{cosθ}$,
∴f(θ)=-8cos2θ+8cosθ+4;
(2)由(1)知,使折线ACD最长即是f(θ)的最大值.
∵f(θ)的最大值为其顶点,此时cosθ=-$\frac{8}{2×(-8)}$=$\frac{1}{2}$,
且0≤θ≤π,
∴θ=60°,
则有:OA=OC=AC=4米,
∴OD=OC•sin60°=2$\sqrt{3}$,
即点D应设计在距离O点2$\sqrt{3}$米处.
点评 本题考查应用三角恒等变换及三角函数知识解决实际问题,首先需要将实际问题通过转化构造出相关的函数关系,其次要能够结合所学三角函数的知识去求最值,本题体现了三角函数的应用价值,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
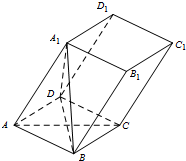 在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
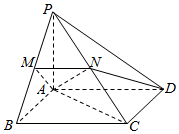 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M、N分别为线段PB,PC 上的点,MN⊥PB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M、N分别为线段PB,PC 上的点,MN⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
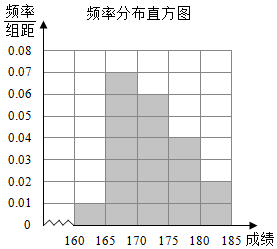 某高校在2015年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示
某高校在2015年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:选择题
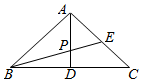 如图,等腰直角三角形ABC中,∠BAC=90°,D为BC的中点,BE平分∠ABC,AD与BE交于点P,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ等于( )
如图,等腰直角三角形ABC中,∠BAC=90°,D为BC的中点,BE平分∠ABC,AD与BE交于点P,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ等于( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{2-\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com