Question

实数m分别取什么数时，复数z=(1+i)m²+(5-2i)m+6-15i是①实数；②虚数；③纯虚数；④对应的点在第三象限；⑤对应的点在直线x+y+4=0上；⑥共轭复数的虚部为12.

Answer 1

解析：z=(1+i)m²+(5-2i)m+6-15i=(m²+5m+6)+(m²-2m-15)i.

∵m∈R，∴z的实部为m²+5m+6,虚部为m²-2m-15.

①要使z为实数，必有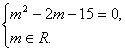

∴m=5或m=-3；

②要使z为虚数，必有m²-2m-15≠0,

∴m≠5且m≠-3；

③要使z为纯虚数，必有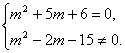

即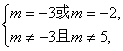∴m=-2；

④要使z对应的点在第三象限，必有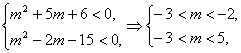

∴-3＜m＜-2；

⑤要使z对应的点在直线x+y+4=0上，必有点（m²+5m+6,m²-2m-15）满足方程x+y+4=0,∴(m²+5m+6)+(m²-2m-15)+4=0.解得m=-或m=1；

⑥要使z的共轭复数的虚部为12，则?-(m²-2m-15)=12,∴m=-1或m=3.