
 若满足地f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
若满足地f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 . ,
, ,动点P(x,y)同时满足
,动点P(x,y)同时满足 则z=x+y的最大值是 .
则z=x+y的最大值是 . 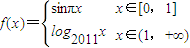 的图象,根据f(a)=f(b)=f(c),不妨a<b<c,结合图象求出a+b+c的范围即可.
的图象,根据f(a)=f(b)=f(c),不妨a<b<c,结合图象求出a+b+c的范围即可.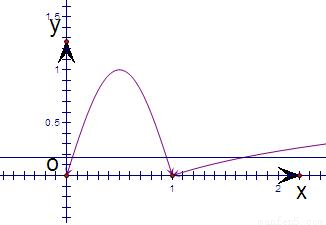 解:(理)作出函数f(x)的图象如图,
解:(理)作出函数f(x)的图象如图,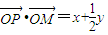 ,
,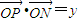
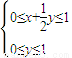
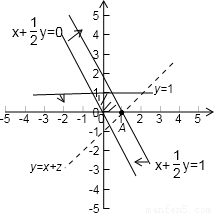 画出可行域
画出可行域 ,1)时,纵截距最大,z最大将(
,1)时,纵截距最大,z最大将( ,1)代入z=x+y得到z的最大值
,1)代入z=x+y得到z的最大值



科目:高中数学 来源: 题型:
|
| OM |
| 1 |
| 2 |
| ON |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州市宝应中学高三数学自主训练试卷(21)(解析版) 题型:填空题
 若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .查看答案和解析>>
科目:高中数学 来源:2011年上海普陀区高考数学三模试卷(文理合卷)(解析版) 题型:解答题
 若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com