
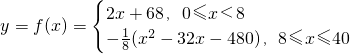
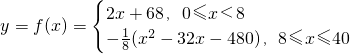 ,
, (x2-32x-480)≥80,
(x2-32x-480)≥80, ≈26.
≈26. <24,∴t∈[0,6],
<24,∴t∈[0,6], ,
, -16≈4.
-16≈4. (x2-32x-480)≥80,由此能够推导出在一节40分钟的课中学生处于“理想听课状态”所持续的时间.
(x2-32x-480)≥80,由此能够推导出在一节40分钟的课中学生处于“理想听课状态”所持续的时间. <24,知t∈[0,6],要学生的注意力指数最低值达到最大,只需f(t)=f(t+24),由此推导出教师上课后从第4分钟开始讲解这道题,能使学生的注意力指数最低值达到最大.
<24,知t∈[0,6],要学生的注意力指数最低值达到最大,只需f(t)=f(t+24),由此推导出教师上课后从第4分钟开始讲解这道题,能使学生的注意力指数最低值达到最大.

 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2013年上海市闵行区高考数学一模试卷(理科)(解析版) 题型:解答题
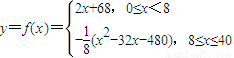
查看答案和解析>>
科目:高中数学 来源:2013年上海市闵行区高考数学一模试卷(文科)(解析版) 题型:解答题
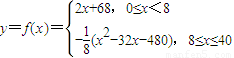
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com