
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=BC=CC1=2,AC=2 ![]() ,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为 .
,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为 . 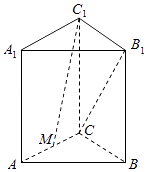
【答案】![]()
【解析】解:在直三棱柱ABC﹣A1B1C1中,AB=BC=CC1=2,AC=2 ![]() ,M是AC的中点,
,M是AC的中点,
∴BM⊥AC,BM= ![]() =1,
=1,
以M为原点,MA为x轴,MB为y轴,过M作AC的垂线为z轴,建立空间直角坐标系,
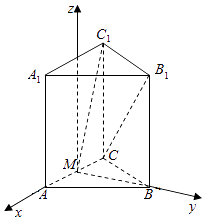
C(﹣ ![]() ,0,0),B1(0,1,2),C1(﹣
,0,0),B1(0,1,2),C1(﹣ ![]() ,0,2),M(0,0,0),
,0,2),M(0,0,0),
![]() =(
=( ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,0,2),
,0,2),
设异面直线CB1与C1M所成角为θ,
则cosθ= 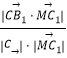 =
= ![]() =
= ![]() .
.
∴异面直线CB1与C1M所成角的余弦值为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=nx﹣xn , x∈R,其中n∈N , 且n≥2.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设曲线y=f(x)与x轴正半轴的交点为P,曲线在点P处的切线方程为y=g(x),求证:对于任意的正实数x,都有f(x)≤g(x);
(Ⅲ)若关于x的方程f(x)=a(a为实数)有两个正实数根x1 , x2 , 求证:|x2﹣x1|< ![]() +2.
+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东佛山某学校参加暑假社会实践活动知识竞赛的学生中,得分在[80,90)中的有16人,得分在[90,100]中的有4人,用分层抽样的方法从得分在[80,100]的学生中抽取一个容量为5的样本,将该样本看成一个整体,从中任意选取2人,则其中恰有1人分数不低于90的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)上的单调函数f(x),对任意的x∈(0,+∞)都有f[f(x)﹣log2x]=3,若方程f(x)+f′(x)=a有两个不同的实数根,则实数a的取值范围是( )
A.(1,+∞)
B.(2+ ![]() ,+∞)
,+∞)
C.(2﹣ ![]() ,+∞)
,+∞)
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )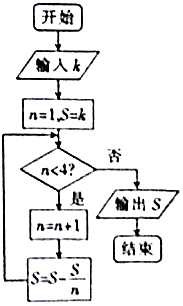
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.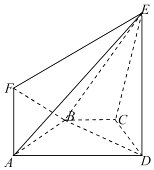
(1)证明:平面ABE⊥平面EBD;
(2)若三棱锥 A﹣BDE的外接球的体积为 ![]() ,求三棱锥 A﹣BEF的体积.
,求三棱锥 A﹣BEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,AC=2,A=120°, ![]() .
.
(Ⅰ)求边AB的长;
(Ⅱ)设(3,4)是BC边上一点,且△ACD的面积为 ![]() ,求∠ADC的正弦值.
,求∠ADC的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}及{bn}中,an+1=an+bn+ ![]() =1.设
=1.设 ![]() ,则数列{cn}的前n项和为( )
,则数列{cn}的前n项和为( )
A.![]()
B.2n+2﹣4
C.3×2n+2n﹣4
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com