
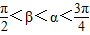 ,且cos(α-β)=
,且cos(α-β)=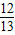 sin(α+β)=-
sin(α+β)=- ,求:cos2α的值.
,求:cos2α的值.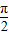 <β<α<
<β<α<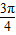 ,∴0<α-β<
,∴0<α-β<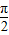 ,π<α+β<
,π<α+β<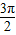 ,
,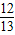 ,sin(α+β)=-
,sin(α+β)=- ,
,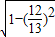 =
=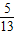 ,cos(α+β)=-
,cos(α+β)=- =-
=- ,
,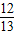 ×(-
×(- )-(-
)-(- )×
)×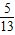 =-
=-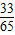 .
.

科目:高中数学 来源:天津市新人教A版数学2012届高三单元测试17:任意角的三角函数 新人教A版 题型:013
已知![]() ,且|cosα|+cosα=0,则tanα=
,且|cosα|+cosα=0,则tanα=
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省天水一中高一(下)期末数学试卷(理科)(解析版) 题型:解答题
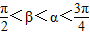 ,且cos(α-β)=
,且cos(α-β)=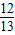 sin(α+β)=-
sin(α+β)=- ,求:cos2α的值.
,求:cos2α的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com