
在![]() 平面上有一系列的点
平面上有一系列的点![]() , 对于正整数
, 对于正整数![]() ,点
,点![]() 位于函数
位于函数![]() 的图像上,以点
的图像上,以点![]() 为圆心的
为圆心的![]() 与
与![]() 轴相切,且
轴相切,且![]() 与
与![]() 又彼此外切,若
又彼此外切,若![]() ,且
,且![]()
(1)求证:数列![]() 是等差数列;w.w.w.k.s.5.u.c.o.m
是等差数列;w.w.w.k.s.5.u.c.o.m ![]()
(2)设![]() 的面积为
的面积为![]() ,
,![]() 求证:
求证:![]()
解析:(1)证明:![]() 的半径为
的半径为![]() ,
,![]() 的半径为
的半径为![]() ,………1分
,………1分
![]() 和
和![]() 两圆相外切,则
两圆相外切,则![]() …………………………2分
…………………………2分
即 ![]() ………………3分
………………3分
整理,得![]() ………………5分
………………5分
又![]() 所以
所以 ![]() ………………………………6分
………………………………6分
即![]() 故数列
故数列![]() 是等差数列 ………………………………7分w.w.w.k.s.5.u.c.o.m
是等差数列 ………………………………7分w.w.w.k.s.5.u.c.o.m ![]()
(2)由(1)得![]() 即
即![]() , ………………8分
, ………………8分
又![]() 所以
所以![]() ………………………9分
………………………9分
法(一):![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() ………………11分
………………11分
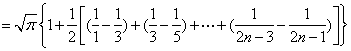 ……13分
……13分
![]() ………………………………14分
………………………………14分
法(二):![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() ………………10分
………………10分
![]() …………………………………………11分
…………………………………………11分
![]()
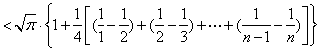 ……………12分
……………12分
![]() ……………………………13分
……………………………13分
![]() …………………………………………14分
…………………………………………14分


科目:高中数学 来源: 题型:
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
在![]() 平面上有一系列的点
平面上有一系列的点![]() , 对于正整数
, 对于正整数![]() ,点
,点![]() 位于函数
位于函数![]() 的图像上,以点
的图像上,以点![]() 为圆心的
为圆心的![]() 与
与![]() 轴相切,且
轴相切,且![]() 与
与![]() 又彼此外切,若
又彼此外切,若![]() ,且
,且![]()
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设![]() 的面积为
的面积为![]() ,
,![]() 求证:
求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
在![]() 平面上有一系列的点
平面上有一系列的点![]() , 对于正整数
, 对于正整数![]() ,点
,点![]() 位于函数
位于函数![]() 的图像上,以点
的图像上,以点![]() 为圆心的
为圆心的![]() 与
与![]() 轴相切,且
轴相切,且![]() 与
与![]() 又彼此外切,若
又彼此外切,若![]() ,且
,且![]()
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设![]() 的面积为
的面积为![]() ,
,![]() 求证:
求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分) ![]() 在
在![]() 平面上有一系列的点
平面上有一系列的点![]() , 对于正整数
, 对于正整数![]() ,点
,点![]() 位于函数
位于函数![]() 的图像上,以点
的图像上,以点![]() 为圆心的
为圆心的![]() 与
与![]() 轴相切,且
轴相切,且![]() 与
与![]() 又彼此外切,若
又彼此外切,若![]() ,且
,且![]()
![]() (1)求证:数列
(1)求证:数列![]() 是等差数列;
是等差数列;![]() (2)设
(2)设![]() 的面积为
的面积为![]() ,
,![]() 求证:
求证:![]()
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com