
|
| A、4 | B、3 | C、2 | D、1 |
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
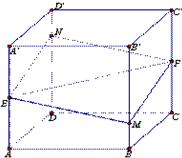 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下四个命题:| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”可信程度越大 |
| B、用相关指数R2来刻画回归的效果时,R2的值越大,说明模型拟合的效果越好 |
| C、残差平方和越大的模型,拟合效果越好 |
| D、作残差图时纵坐标可以是解释变量,也可以是预报变量 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三二诊模拟文科数学试卷(解析版) 题型:解答题
已知函数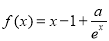 (
(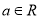 ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线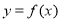 在点
在点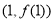 处的切线平行于
处的切线平行于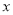 轴,求
轴,求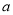 的值;
的值;
(2)求函数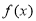 的极值;
的极值;
(3)当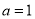 的值时,若直线
的值时,若直线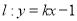 与曲线
与曲线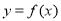 没有公共点,求
没有公共点,求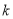 的最大值.
的最大值.
(注:可能会用到的导数公式: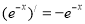 ;
;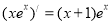 )
)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟文科数学试卷(解析版) 题型:解答题
已知椭圆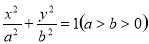 的离心率为
的离心率为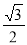 ,点
,点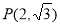 在椭圆上.
在椭圆上.
(1)求椭圆C的方程;
(2)设椭圆的左右顶点分别是A、B,过点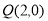 的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.
的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com