
| 3 |
| 3 |
| ||
| 2 |
| 5 |
| 1 |
| 4 |
|
| y1-y0 |
| x1-x0 |
| y1+y0 |
| x1+x2 |
| y12-y02 |
| x12-x02 |
| 1 |
| 4 |
|
| x2 |
| 4 |
| x2 |
| 4 |
| m |
| 3 |
| 5 |
| m |
| 3 |
| 5 |
| m |
| 3 |
| m |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| y1-y0 |
| x1-x0 |
| y1+y0 |
| x1+x0 |
| y1-y0 |
| x1-x0 |
| y1+y0 |
| x1+x2 |
| y12-y02 |
| x12-x02 |
|
| y12-y02 |
| x12-x02 |
| 1 |
| 4 |
| 1 |
| 4 |


科目:高中数学 来源: 题型:
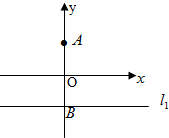 已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某海海岸线可以近似的看成直线,位于岸边A处 的海警发现海中B处有人求救,该海警没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若海警在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒,(不考虑水流速度等因素)
某海海岸线可以近似的看成直线,位于岸边A处 的海警发现海中B处有人求救,该海警没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若海警在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒,(不考虑水流速度等因素)查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
A、(-
| ||
| B、(4,6) | ||
| C、(2,4) | ||
D、(-3,-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知F1、F2为为双曲线C:
已知F1、F2为为双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com