
 具有以下性质:①
具有以下性质:① ②若
②若 ,则
,则 ,且
,且 时,
时, .则称集合
.则称集合 是“好集”.
是“好集”. ,有理数集Q是否是“好集”,并说明理由;
,有理数集Q是否是“好集”,并说明理由; 是“好集”,求证:若
是“好集”,求证:若 ,则
,则 ;
; :若
:若 ,则必有
,则必有 ;
; :若
:若 ,且
,且 ,则必有
,则必有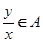 ;
; 是“好集”. (Ⅱ)
是“好集”. (Ⅱ)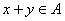 .
.  均为真命题..
均为真命题..  是“好集”.因为
是“好集”.因为 ,
, ,所以
,所以
 矛盾.这样就确定集合
矛盾.这样就确定集合 不是“好集”.有理数Q也采用同样的方法,进行推证.
不是“好集”.有理数Q也采用同样的方法,进行推证. 是“好集”,则
是“好集”,则 ,然后再根据x,y的任意性,可证明
,然后再根据x,y的任意性,可证明 .
. 不是“好集”. 理由是:假设集合
不是“好集”. 理由是:假设集合 是“好集”.
是“好集”.  ,
, ,所以
,所以 . 这与
. 这与 矛盾.…………2分
矛盾.…………2分 是“好集”. 因为
是“好集”. 因为 ,
, ,对任意的
,对任意的 ,有
,有 ,且
,且 时,
时, .所以有理数集
.所以有理数集 是“好集”. ………………………………4分
是“好集”. ………………………………4分 是“好集”,所以
是“好集”,所以  .若
.若 ,则
,则 ,即
,即 .
. ,即
,即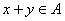 . …………………………6分
. …………………………6分 均为真命题. 理由如下: ………………………………………7分
均为真命题. 理由如下: ………………………………………7分 ,任取
,任取 , 若
, 若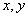 中有0或1时,显然
中有0或1时,显然 .
.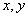 均不为0,1. 由定义可知:
均不为0,1. 由定义可知: .所以
.所以 ,即
,即 .
.  . 由(Ⅱ)可得:
. 由(Ⅱ)可得: ,即
,即 . 同理可得
. 同理可得 .
. 或
或 ,则显然
,则显然 .若
.若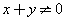 且
且 ,则
,则 .
. . 所以
. 所以  .由(Ⅱ)可得:
.由(Ⅱ)可得: .
. .综上可知,
.综上可知, ,即命题
,即命题 为真命题.若
为真命题.若 ,且
,且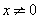 ,则
,则 .
. ,即命题
,即命题 为真命题. ……………………………………13分
为真命题. ……………………………………13分 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题
 关于运算
关于运算 满足:
满足: ,都有
,都有 ;
; ,使得对一切
,使得对一切 ,都有
,都有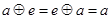 ,则称
,则称 关于运算
关于运算 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:
 ① ②
① ②
 ④
④  ⑤
⑤ 关于运算
关于运算 为“融洽集”____________。(写出所有“融洽集”的序号)
为“融洽集”____________。(写出所有“融洽集”的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com