
设![]() 分别为椭圆
分别为椭圆![]() 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1,![]() )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4.
⑴写出椭圆C的方程和焦点坐标;
⑵过点P(1,![]() )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
⑶过点Q(1,0)的直线与椭圆交于两点M、N,若△OMN面积取得最大,求直线MN的方程.
⑴椭圆C的焦点在x轴上,由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.;
又点A(1,![]() ) 在椭圆上,因此
) 在椭圆上,因此 得b2=1,于是c2=3;所以椭圆C的方程为
得b2=1,于是c2=3;所以椭圆C的方程为![]() ,⑵∵P在椭圆内,∴直线DE与椭圆相交,∴设D(x1,y1),E(x2,y2),代入椭圆C的方程得 x12+4y12-4=0, x22+4y22-4=0,相减得2(x1-x2)+4×2×
,⑵∵P在椭圆内,∴直线DE与椭圆相交,∴设D(x1,y1),E(x2,y2),代入椭圆C的方程得 x12+4y12-4=0, x22+4y22-4=0,相减得2(x1-x2)+4×2×![]() (y1-y2)=0,∴斜率为k=-1
(y1-y2)=0,∴斜率为k=-1
∴DE方程为y-1= -1(x-![]() ),即4x+4y=5;
),即4x+4y=5;
(3)直线MN不与y轴垂直,∴设MN方程为my=x-1,代入椭圆C的方程得
(m2+4)y2+2my-3=0, 设M(x1,y1),N(x2,y2),则y1+y2=-![]() , y1y2=-
, y1y2=-![]() ,且△>0成立.
,且△>0成立.
又S△OMN=![]() |y1-y2|=
|y1-y2|=![]() ×
×![]() =
=![]() ,设t=
,设t=![]() ≥
≥![]() ,则
,则
S△OMN=![]() ,(t+
,(t+![]() )′=1-t-2>0对t≥
)′=1-t-2>0对t≥![]() 恒成立,∴t=
恒成立,∴t=![]() 时t+
时t+![]() 取得最小,S△OMN最大,
取得最小,S△OMN最大,
此时m=0,∴MN方程为x=1


科目:高中数学 来源:2014届浙江省高二下学期期中文科数学试卷(解析版) 题型:选择题
设 分别为椭圆
分别为椭圆 的左、右焦点,点A,B在椭圆上,若
的左、右焦点,点A,B在椭圆上,若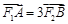 ,
,
则点A的坐标是( )
A. B.
B. C.
C.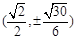 D.
D.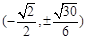
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省武汉市武昌区高三五月调研理科数学试卷(解析版) 题型:选择题
设 分别为椭圆
分别为椭圆 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 的点
的点 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是
A.
 B.
B. C.
C.
 D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第四次月考理科数学试卷 题型:解答题
设 ,
, 分别为椭圆
分别为椭圆
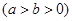 的左、右焦点,过
的左、右焦点,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的倾斜角为
的倾斜角为 ,
, 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的焦距;
的焦距;
(2)如果 ,求椭圆
,求椭圆 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷十二文科数学 题型:解答题
设 分别为椭圆
分别为椭圆 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且 为它的右准线.
为它的右准线.
(Ⅰ)求椭圆的方程;
(Ⅱ)设 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线 分别与椭圆相交于异于
分别与椭圆相交于异于 的点
的点 ,证明点
,证明点 在以
在以 为直径的圆内.
为直径的圆内.
(此题不要求在答题卡上画图)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com